题目内容
13．过抛物线y+2x2=0的焦点的直线交抛物线于A、B两点．则xAxB=-$\frac{1}{16}$．分析 求得抛物线的焦点，设出过焦点的直线，代入抛物线方程，消去y，得到x的方程，由韦达定理，即可得到所求．
解答 解：抛物线y+2x2=0即为x2=-$\frac{1}{2}$y，
焦点为（0，-$\frac{1}{8}$），
设过焦点的直线为y=kx-$\frac{1}{8}$，
联立抛物线方程y=-2x2，
则2x2+kx-$\frac{1}{8}$=0，
即有xAxB=-$\frac{1}{16}$，
故答案为：-$\frac{1}{16}$．
点评 本题考查抛物线的方程和性质，考查直线方程和抛物线方程联立，运用韦达定理，考查运算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
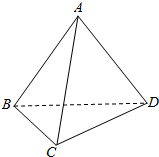如图，在三棱锥A-BCD中，AB=BC=CD=DA=AC，BD=$\sqrt{2}$AB，求证：平面ABD⊥平面BCD．
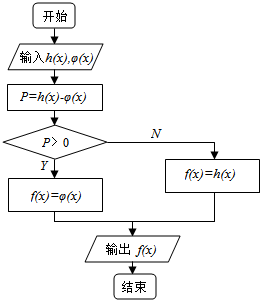函数f（x）的定义由程序框图给出，程序运行时，输入h（x）=（$\frac{1}{2}$）x，φ（x）=log2x，则f（$\frac{1}{2}$）+f（4）的值为-$\frac{15}{16}$．
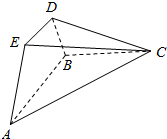已知△ABC为直角三角形，AB⊥BC，四边形ABDE为等腰梯形，DE∥AB，平面ABDE⊥平面ABC，AB=BC=2DE=2．