题目内容
11.枣庄市教育局基教科研本市高中学生的性别与阅读量、智商、视力、成绩这四个变量只剪断额关系,在全是高中学校随机抽查了20名男生、30名女生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )| 阅读量 性别 | 丰富 | 不丰富 |
| 男 | 14 | 6 |
| 女 | 4 | 26 |
| 智商 性别 | 偏高 | 正常 |
| 男 | 8 | 12 |
| 女 | 8 | 22 |
| 视力 性别 | 好 | 差 |
| 男 | 5 | 15 |
| 女 | 12 | 18 |
| 成绩 性别 | 不及格 | 及格 |
| 男 | 6 | 14 |
| 女 | 10 | 20 |
| A. | 阅读量 | B. | 智商 | C. | 视力 | D. | 成绩 |
分析 根据表中数据,利用公式,求出X2,即可得出结论.
解答 解:表1:X2=$\frac{50×(14×26-4×6)^{2}}{18×32×20×30}$≈16.7;
表2:X2=$\frac{50×(8×22-12×8)^{2}}{16×34×20×30}$≈0.98;
表3:X2=$\frac{50×(5×18-12×15)^{2}}{17×33×20×30}$≈1.203;
表4:X2=$\frac{50×(6×20-10×14)^{2}}{16×34×20×30}$≈0.06,
∴阅读量与性别有关联的可能性最大,
故选:A.
点评 本题考查独立性检验的应用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.定义新运算“a※b”为a※b=$\left\{{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}}\right.$,例如1※2=1,3※2=2,则函数f(x)=sinx※cosx的值域是( )
| A. | $[-1,\frac{{\sqrt{2}}}{2}]$ | B. | $[0,\frac{{\sqrt{2}}}{2}]$ | C. | [-1,1] | D. | $[-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}]$ |
6.下列命题中的真命题的个数是( )
①a>b成立的一个充分不必要的条件是a>b+1;
②已知命题p∨q为真命题,则p∧q为真命题;
③命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
④命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-3x+2≤0”.
①a>b成立的一个充分不必要的条件是a>b+1;
②已知命题p∨q为真命题,则p∧q为真命题;
③命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
④命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-3x+2≤0”.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.(B题)某射击运动员一次射击所得环数X的分布如下:
现进行三次射击,以该运动员三次射击所得环数最高环数作为他的成绩,记为Y.
(Ⅰ)求该运动员三次都命中8环的概率;
(Ⅱ)求Y的分布及平均值(期望)EY.
| X | 8 | 9 | 10 |
| P | 0.3 | 0.5 | 0.2 |
(Ⅰ)求该运动员三次都命中8环的概率;
(Ⅱ)求Y的分布及平均值(期望)EY.
1.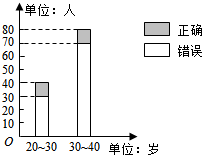 “开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(Ⅰ) 完成2×2列联表;
(Ⅱ)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
(参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$,n=n1++n2++n+1+n+2)
 “开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.(Ⅰ) 完成2×2列联表;
正误 年龄 | 正确 | 错误 | 合计 |
| 20~30 | |||
| 30~40 | |||
| 合计 |
| P(Χ2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |