题目内容
已知函数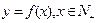 ,满足:①对任意
,满足:①对任意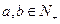 ,都有
,都有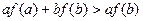
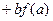 ;
;
②对任意n∈N *都有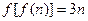 .
.
(Ⅰ)试证明: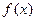 为
为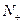 上的单调增函数;
上的单调增函数;
(Ⅱ)求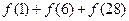 ;
;
(Ⅲ)令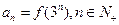 ,试证明:
,试证明: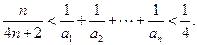
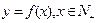 ,满足:①对任意
,满足:①对任意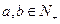 ,都有
,都有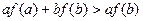
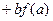 ;
;②对任意n∈N *都有
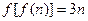 .
. (Ⅰ)试证明:
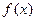 为
为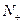 上的单调增函数;
上的单调增函数;(Ⅱ)求
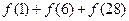 ;
;(Ⅲ)令
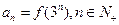 ,试证明:
,试证明: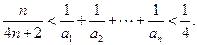
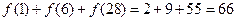
解:(I) 由①知,对任意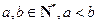 ,都有
,都有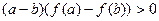 ,
,
由于 ,从而
,从而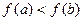 ,所以函数
,所以函数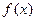 为
为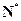 上的单调增函数
上的单调增函数
(II)令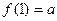 ,则
,则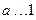 ,显然
,显然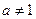 ,否则
,否则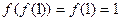 ,与
,与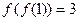 矛盾.从而
矛盾.从而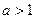 ,而由
,而由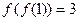 ,即得
,即得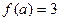 .
.
又由(I)知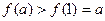 ,即
,即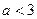 .
.
于是得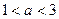 ,又
,又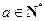 ,从而
,从而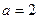 ,即
,即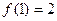 .
.
进而由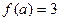 知,
知,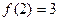 .
.
于是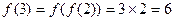 ,
,
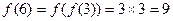 ,
, 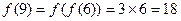 ,
,
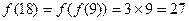 ,
, 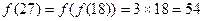 ,
,
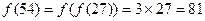 , 由于
, 由于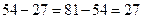 ,
,
而且由(I)知,函数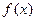 为单调增函数,因此
为单调增函数,因此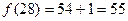 .
.
从而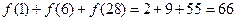 .
.
(Ⅲ)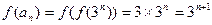 ,
,
 ,
,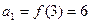 .
.
即数列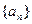 是以6为首项, 以3为公比的等比数列 .
是以6为首项, 以3为公比的等比数列 .
∴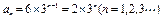
于是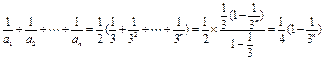 ,显然
,显然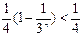 ,
,
另一方面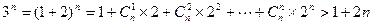 ,
,
从而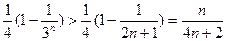 .
.
综上所述,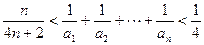 .
.
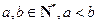 ,都有
,都有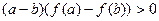 ,
,由于
 ,从而
,从而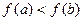 ,所以函数
,所以函数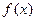 为
为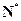 上的单调增函数
上的单调增函数 (II)令
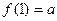 ,则
,则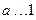 ,显然
,显然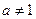 ,否则
,否则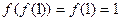 ,与
,与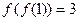 矛盾.从而
矛盾.从而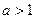 ,而由
,而由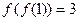 ,即得
,即得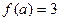 .
.又由(I)知
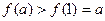 ,即
,即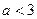 .
.于是得
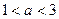 ,又
,又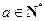 ,从而
,从而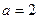 ,即
,即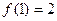 .
.进而由
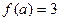 知,
知,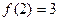 .
.于是
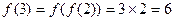 ,
, 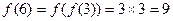 ,
, 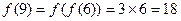 ,
,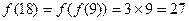 ,
, 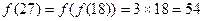 ,
,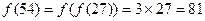 , 由于
, 由于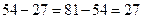 ,
,而且由(I)知,函数
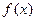 为单调增函数,因此
为单调增函数,因此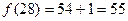 .
.从而
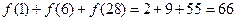 .
. (Ⅲ)
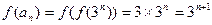 ,
, ,
,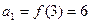 .
.即数列
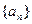 是以6为首项, 以3为公比的等比数列 .
是以6为首项, 以3为公比的等比数列 . ∴
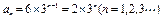
于是
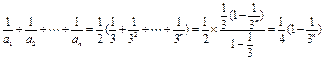 ,显然
,显然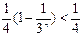 ,
, 另一方面
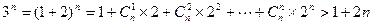 ,
,从而
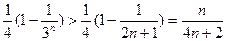 .
. 综上所述,
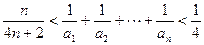 .
. 
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 形ABC,AB=
形ABC,AB=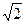 ,点E是
,点E是 斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为
斜边AB上的动点,过E点做矩形EFCG,设矩形EFCG面积为S,矩形一边EF长为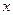 ,
,
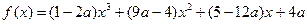 (
(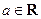 ).
).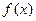 的单调递增区间;
的单调递增区间; 中,满足 “对
中,满足 “对 ,当
,当 时,都有
时,都有 ”的是
”的是 B.
B. C.
C. D.
D.




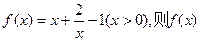 ( )
( )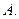 有最小值
有最小值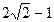
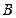 .有最大值
.有最大值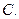 有最大值
有最大值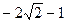
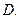 有最大值
有最大值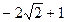
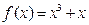 ,则
,则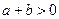 是
是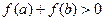 的( )
的( ) ,则S的最小值是_______ _______
,则S的最小值是_______ _______ 的部分对应值如下表:
的部分对应值如下表: 的解集是 。
的解集是 。