题目内容
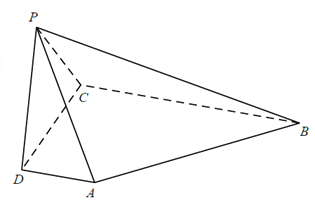
【题目】已知函数f(x)=ax﹣lnx;g(x)= ![]() .
.
(1)讨论函数f(x)的单调性;
(2)求证:若a=e(e是自然常数),当x∈[1,e]时,f(x)≥e﹣g(x)恒成立;
(3)若h(x)=x2[1+g(x)],当a>1时,对于x1∈[1,e],x0∈[1,e],使f(x1)=h(x0),求a的取值范围.
【答案】
(1)解:∵f(x)=ax﹣lnx,∴x>0, ![]() ,
,
∵x>0,
∴当a≤0时,f′(x)<0,∴f(x)在(0,+∞)上是减函数,
当a>0时,若x> ![]() ,则f′(x)>0,∴f(x)在(
,则f′(x)>0,∴f(x)在( ![]() ,+∞)上是增函数,
,+∞)上是增函数,
若0<x< ![]() ,则f′(x)<0,∴f(x)在(0,
,则f′(x)<0,∴f(x)在(0, ![]() )上是减函数.
)上是减函数.
综上所述,当a≤0时,f(x)在(0,+∞)上是减函数,
当a>0时,f(x)在( ![]() ,+∞)上是增函数,在(0,
,+∞)上是增函数,在(0, ![]() )上是减函数.
)上是减函数.
(2)证明:当a=e时,f(x)=ex﹣lnx,
∴ ![]() ,∴x∈[1,e]时,f′(x)>0恒成立.
,∴x∈[1,e]时,f′(x)>0恒成立.
f(x)=ex﹣lnx在[1,e]上是单调递增函数,∴f(x)min=f(1)=e,
令H(x)=e﹣g(x)=e﹣ ![]() ,则H′(x)=
,则H′(x)= ![]() ,x∈[1,e]时,H′(x)≤0,
,x∈[1,e]时,H′(x)≤0,
∴H(x)在[1,e]上单调递减,H(x)max=H(1)=e,
∴f(x)≥H(x),即f(x)≥e﹣g(x).
故a=e(e是自然常数),当x∈[1,e]时,f(x)≥e﹣g(x)恒成立.
(3)解:∵ ![]() ,a>1时,由x∈[1,e],得f′(x)>0,
,a>1时,由x∈[1,e],得f′(x)>0,
∴f(x)=ax﹣lnx在[1,e]上单调递增,
f(x)min=f(1)=a,f(x)max=f(e)=ae﹣1,即f(x)的值域是[a,ae﹣1],
由h(x)=x2+1﹣lnx,得 ![]() ,∴x∈[1,e]时,h′(x)>0,
,∴x∈[1,e]时,h′(x)>0,
h(x)在[1,e]上单调递增,
∴h(x)min=h(1)=2,h(x)max=h(e)=e2,即h(x)的值域是[2,e2],
x1∈[1,e],x0∈[1,e],有f(x1)=h(x0),
∴f(x)的值域是h(x)的值域的子集,
∴ ![]() ,∴
,∴ ![]() .
.
∴a的取值范围是[2,e+ ![]() ].
].
【解析】(1)推导出 ![]() ,由此利用导数性质能讨论函数f(x)的单调性.(2)当a=e时,f(x)=ex﹣lnx,
,由此利用导数性质能讨论函数f(x)的单调性.(2)当a=e时,f(x)=ex﹣lnx, ![]() ,由此利用构造法和导数性质能证明a=e(e是自然常数),当x∈[1,e]时,f(x)≥e﹣g(x)恒成立.(3)由
,由此利用构造法和导数性质能证明a=e(e是自然常数),当x∈[1,e]时,f(x)≥e﹣g(x)恒成立.(3)由 ![]() ,a>1时,求出f(x)的值域是[a,ae﹣1],由此利用导数性质能求出a的取值范围.
,a>1时,求出f(x)的值域是[a,ae﹣1],由此利用导数性质能求出a的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年利润y(单位:万元)的影响,对近5年的宣传费xi和年利润yi(i=1,2,3,4,5)进行了统计,列出了下表:
x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程: ![]() =1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据
=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据 ![]() (yi﹣
(yi﹣ ![]() i)2=1.15) 参考公式:相关指数R2=1﹣
i)2=1.15) 参考公式:相关指数R2=1﹣ 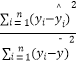
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ![]() =
= 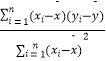 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x,参考数据:ln40=3.688,
x,参考数据:ln40=3.688, ![]() =538.
=538.