题目内容
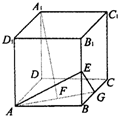 如图正方体ABCD-A1B1C1D1中,E、F、G分别是B1B、AB、BC的中点.
如图正方体ABCD-A1B1C1D1中,E、F、G分别是B1B、AB、BC的中点.(1)证明:D1F⊥平面AEG;
(2)求cos<
| AE |
| D1B |
分析:(1)如图以D为原点,DA、DC、DD1所在的直线分别为x、y、z轴,求出D1F与EG1的方向向量,根据向量的数量积为0,两个向量垂直得到D1F⊥EG,D1F⊥AE.结合线面垂直的判定定理可得D1F⊥平面AEG.
(2)由 由
=(0,a,),
=(a,a,-a),代入向量夹角公式可得cos<
,
>.
(2)由 由
| AE |
| D1B |
| AE |
| D1B |
解答: 解:以D为原点,DA、DC、DA1所在的直线分别为x、y、z轴,
解:以D为原点,DA、DC、DA1所在的直线分别为x、y、z轴,
建立空间直角坐标系,设正方体AC1棱长为a,则D(0,0,0),
A(a,0,0),B(a,a,0),D1(0,0,a),E(a,a,
),
F(a,
,0),G(
,a,0).
(1)
=(0,a,
),∴
•
=a×0+
×a-a×
=0
∴D1F⊥AE,
同理D1F⊥EG
∵EG∩AE=E,∴D1F⊥平面AEG.
(2)由
=(0,a,),
=(a,a,-a)
∴cos<
,
>=
=
=
.
 解:以D为原点,DA、DC、DA1所在的直线分别为x、y、z轴,
解:以D为原点,DA、DC、DA1所在的直线分别为x、y、z轴,建立空间直角坐标系,设正方体AC1棱长为a,则D(0,0,0),
A(a,0,0),B(a,a,0),D1(0,0,a),E(a,a,
| a |
| 2 |
F(a,
| a |
| 2 |
| a |
| 2 |
(1)
| AE |
| a |
| 2 |
| D1F |
| AE |
| a |
| 2 |
| a |
| 2 |
∴D1F⊥AE,
同理D1F⊥EG
∵EG∩AE=E,∴D1F⊥平面AEG.
(2)由
| AE |
| D1B |
∴cos<
| AE |
| D1B |
| ||||
|
|
a2-
| ||||||
|
| ||
| 15 |
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面垂直的判定,直线与平面所成的角,点、线、面间的距离计算,是立体几何的一个综合考查,难度稍大.

练习册系列答案
相关题目
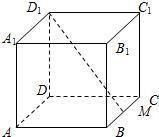 如图正方体ABCD-A1B1C1D1中,M为BC中点,则直线D1M与平面ABCD所成角的正切值为
如图正方体ABCD-A1B1C1D1中,M为BC中点,则直线D1M与平面ABCD所成角的正切值为
 如图正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1,BD1的公垂线,并求OM的长.
如图正方体ABCD-A1B1C1D1的棱长为1,点M是棱AA1的中点,点O是BD1的中点,求证:OM是异面直线AA1,BD1的公垂线,并求OM的长. 如图正方体ABCD-A1B1C1D1的棱长为2,则点B1到直线AC的距离是
如图正方体ABCD-A1B1C1D1的棱长为2,则点B1到直线AC的距离是 (文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:
(文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中: 甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=
甲.如图1,平面VAD⊥平面ABCD,△VAD是等边三角形,ABCD是矩形,AB:AD=