题目内容
如图正方体ABCD-A1B1C1D1的棱长为2，则点B1到直线AC的距离是| 6 |
| 6 |
分析：设AC∩BD=O，连B1O，则B1O的长就是所求点B1到直线AC的距离，利用解直角三角形，即可得到结论．
解答：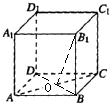
解：设AC∩BD=O，连B1O，
∵AC⊥BD，B1B⊥面ABCD，∴B1O⊥AC，
则B1O的长就是所求点B1到直线AC的距离．
在Rt△BB1O中，BB1=2，BO=
，∴B1O=
．
故答案为：
；
解：设AC∩BD=O，连B1O，∵AC⊥BD，B1B⊥面ABCD，∴B1O⊥AC，
则B1O的长就是所求点B1到直线AC的距离．
在Rt△BB1O中，BB1=2，BO=
| 2 |
| 6 |
故答案为：
| 6 |
点评：本题考查异面直线间距离的计算，考查学生分析解决问题的能力，正确作出B1O是关键．
练习册系列答案
相关题目
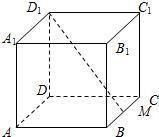如图正方体ABCD-A1B1C1D1中，M为BC中点，则直线D1M与平面ABCD所成角的正切值为
如图正方体ABCD-A1B1C1D1的棱长为1，点M是棱AA1的中点，点O是BD1的中点，求证：OM是异面直线AA1，BD1的公垂线，并求OM的长．
（文）如图正方体ABCD-A1B1C1D1，在它的12条棱及12条面的对角线所在的直线中，选取若干条直线确定平面，在所有的这些平面中：
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=