题目内容
 (文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:
(文)如图正方体ABCD-A1B1C1D1,在它的12条棱及12条面的对角线所在的直线中,选取若干条直线确定平面,在所有的这些平面中:(1)、过B1C且与BD平行的平面有且只有一个;
(2)、过B1C且与BD垂直的平面有且只有一个;
(3)、存在平面α,过B1C与直线BD所成的角等于30.
其中是真命题的个数是( )
分析:(1)先由线面平行的判定定理可证明符合条件的平面有平面B1D1C,再说明它的唯一性;(2)利用反证法,若存在过B1C且与BD垂直的平面α,则BD与B1C所成的角为90°,这与事实BD与B1C所成的角为30°矛盾;(3)可以计算BD与平面A1B1CD所成的角就是30°:连接BC1交B1C于O,证明∠BDO就是直线BD与平面A1B1CD所成的角,进而在直角三角形中计算即可
解答:解:(1)在24条直线中,与直线BD平行的直线只有B1D1,故过B1C且与BD平行的平面有且只有一个即平面B1D1C,故(1)正确;
(2)因为直线BD与直线B1C所成的角即为∠A1DB,已知△A1DB为等边三角形,所以直线BD与直线B1C所成的角为60°,
假设存在过B1C且与BD垂直的平面α,则因为B1C?α,所以BD⊥B1C,这与事实矛盾
故不可能存在过B1C且与BD垂直的平面,(2)错误
(3)连接BC1交B1C于O
∵BC1⊥B1C,CD⊥BC1,B1C∩CD=C
∴BC1⊥平面A1B1CD,即BO⊥平面A1B1CD
∴∠BDO就是直线BD与平面A1B1CD所成的角
在直角三角形BDO中,BD=
a,BO=
a,
∴∠BDO=30°
∴直线BD与平面A1B1CD所成的角为30°
故存在平面α,即平面A1B1CD,过B1C与直线BD所成的角等于30°,(3)正确
故真命题的个数为2
故选C
(2)因为直线BD与直线B1C所成的角即为∠A1DB,已知△A1DB为等边三角形,所以直线BD与直线B1C所成的角为60°,
假设存在过B1C且与BD垂直的平面α,则因为B1C?α,所以BD⊥B1C,这与事实矛盾
故不可能存在过B1C且与BD垂直的平面,(2)错误
(3)连接BC1交B1C于O
∵BC1⊥B1C,CD⊥BC1,B1C∩CD=C
∴BC1⊥平面A1B1CD,即BO⊥平面A1B1CD
∴∠BDO就是直线BD与平面A1B1CD所成的角
在直角三角形BDO中,BD=
| 2 |
| ||
| 2 |
∴∠BDO=30°
∴直线BD与平面A1B1CD所成的角为30°
故存在平面α,即平面A1B1CD,过B1C与直线BD所成的角等于30°,(3)正确
故真命题的个数为2
故选C
点评:本题考查了正方体中的线面关系,线面平行、线面垂直的判定与性质,线面角的计算,具有较强的空间想象能力和推理能力是解决本题的关键

练习册系列答案
相关题目
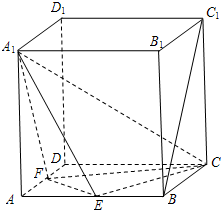 (2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
(2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
 (文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
