题目内容

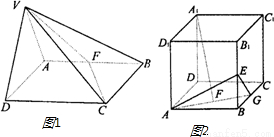
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=
2
：1，F是AB的中点．
（1）求VC与平面ABCD所成的角；
（2）求二面角V-FC-B的度数；
（3）当V到平面ABCD的距离是3时，求B到平面VFC的距离．
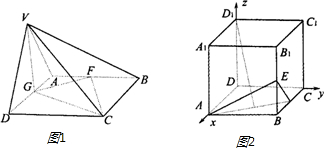
乙、如图正方体ABCD-A1B1C1D1中，E、F、G分别是B1B、AB、BC的中点．
（1）证明：D1F⊥EG；
（2）证明：D1F⊥平面AEG；
（3）求cos＜
AE
，
D1B
＞．
注意：考生在（19甲）、（19乙）两题中选一题作答，如果两题都答，只以（19甲）计分．
分析：甲（1）取AD的中点G连接VG，CG，由等腰三角形三线合一及面面垂直的性质可得VG⊥平面ABCD，即∠VCG为CV与平面ABCD所成的角，解Rt△GDC及Rt△VGC可得VC与平面ABCD所成的角；
（2）连接GF，解△GFC中可得GF⊥FC，连接VF，由VG⊥平面ABCD知VF⊥FC，则∠VFG即为二面角V-FC-D的平面角，解Rt△VFG可得二面角V-FC-B的度数；
（3）设B到平面VFC的距离为h，当V到平面ABCD的距离是3时，即VG=3．根据等体积法即VV-FCB=VB-VCF，可得B到面VCF的距离．
乙
（1）如图2以D为原点，DA、DC、DD1所在的直线分别为x、y、z轴，求出D1F与EG1的方向向量，根据向量的数量积为0，两个向量垂直得到D1F⊥EG．
（2）由向量
AE
=(0，a，
a
2
），根据
D1F
•
AE
=a×0+
a
2
×a-a×
a
2
=0．可得D1F⊥AE．结合（1）的结论及线面垂直的判定定理可得D1F⊥平面AEG．
（3）由
AE
=(0，a，
a
2
），
D1B
=（a，a，-a），代入向量夹角公式可得cos＜
AE
，
D1B
＞
解答：甲
解：（1）取AD的中点G（图1），连接VG，CG．
∵△ADV为正三角形，∴VG⊥AD．
又平面VAD⊥平面ABCD．AD为交线，
∴VG⊥平面ABCD，
则∠VCG为CV与平面ABCD所成的角．
设AD=a，则VG=
3
2
a，DC=
2
a．
在Rt△GDC中，GC=
DC2+GD2
=
2a2+
a2
4
=
3
2
a．
在Rt△VGC中，tan∠VCG=
VG
GC
=
3
3
．
∴∠VCG=30°．
即VC与平面ABCD成30°．
（2）连接GF，则GF=
AG2+AF2
=
3
2
a．
而　FC=
FB2+BC2
=
6
2
a．
在△GFC中，GC2=GF2+FC2．∴GF⊥FC．
连接VF，由VG⊥平面ABCD知VF⊥FC，则∠VFG即为二面角V-FC-D的平面角．
在Rt△VFG中，VG=GF=
3
2
a．
∴∠VFG=45°．　二面角V-FC-B的度数为135°．
（3）设B到平面VFC的距离为h，当V到平面ABCD的距离是3时，即VG=3．
此时AD=BC=2
3
，FB=
6
，FC=3
2
，VF=3
2
．
∴S△VFC=
1
2
VF•FC=9，S△BFC=
1
2
FB•BC=3
2
．
∵VV-FCB=VB-VCF，
∴
1
3
•VG•S△FBC=
1
3
•h•S△VFC．
∴
1
3
×3×3
2
=
1
3
•h•9．
∴h=
2
即B到面VCF的距离为
2
．
乙
解：如图2以D为原点，DA、DC、DD1所在的直线分别为x、y、z轴，建立空间直角坐标系，设正方体AC1棱长为a，则D（0，0，0），A（a，0，0），B（a，a，0），D1（0，0，a），E（a，a，
a
2
），F（a，
a
2
，0），G（
a
2
，a，0）．
（1）
D1F
=(a，
a
2
，-a），
EG
=(-
a
2
，0，-
a
2
)，
∵
D1F
•
EG
=a(-
a
2
)+
a
2
×0+(-a)(-
a
2
)=0，
∴D1F⊥EG．
（2）
AE
=(0，a，
a
2
），
∴
D1F
•
AE
=a×0+
a
2
×a-a×
a
2
=0．
∴D1F⊥AE．
∵EG∩AE=E，∴D1F⊥平面AEG．
（3）由
AE
=(0，a，
a
2
），
D1B
=（a，a，-a），
∴cos＜
AE
，
D1B
＞=
AE
•
D1B
|
AE
|•|
D1B
|
=
a2-
1
2
a2
0+a2+
a2
4
•
a2+a2+(-a)2
=
5
15
．
点评：题考查的知识点是用空间向量求平面间的夹角，直线与平面垂直的判定，直线与平面所成的角，点、线、面间的距离计算，是立体几何的一个综合考查，难度稍大．
练习册系列答案
相关题目
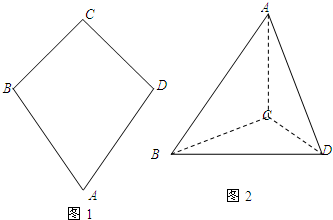
如图1，平面四边形ABCD中，A=
π
3
C=
π
2
，CB=CD=2，且AB=AD．把△ABD沿BD折起（如图2），使二面角A-BD-C的余弦值等于
3
3
对于图二，完成以下各小题：
（1）求AC的长；
（2）证明：AC⊥平面BCD；
（3）求直线AC与平面ABD所成角的正弦值．
如图1，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=90°，CD=2．把△ABD沿BD折起（如图2），使二面角A-BD-C的余弦值等于
3
3
．对于图2：
（Ⅰ）求AC；
（Ⅱ）证明：AC⊥平面BCD；
（Ⅲ）求直线AC与平面ABD所成角的正弦值．
如图1，平面四边形ABCD关于直线AC对称，∠A=60°，∠C=90°，CD=2．把△ABD沿BD折起（如图2），使二面角A-BD-C的余弦值等于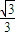．对于图2：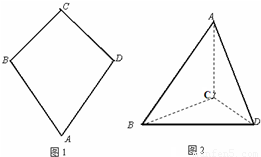
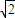（Ⅰ）求AC；
（Ⅱ）证明：AC⊥平面BCD；
（Ⅲ）求直线AC与平面ABD所成角的正弦值．
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=：1，F是AB的中点．
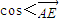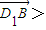（1）求VC与平面ABCD所成的角；
（2）求二面角V-FC-B的度数；
（3）当V到平面ABCD的距离是3时，求B到平面VFC的距离．
乙、如图正方体ABCD-A1B1C1D1中，E、F、G分别是B1B、AB、BC的中点．
（1）证明：D1F⊥EG；
（2）证明：D1F⊥平面AEG；
（3）求，．
注意：考生在（19甲）、（19乙）两题中选一题作答，如果两题都答，只以（19甲）计分．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网