题目内容
将一颗骰子抛掷两次分别得到向上的点数a,b,则直线ax-bx=0与圆x2+(y-5)2=5相切的概率为( )
A.
| B.
| C.
| D.
|
由题意知本题是一个古典概型,试验发生包含的事件是先后两次抛掷一枚骰子,
将得到的点数分别记a,b,则事件总数为6×6=36.
∵直线ax-bx=0与圆x2+(y-5)2=5相切的充要条件是
=
即a2=4b2,即a=2b
∵a、b∈{1,2,3,4,5,6}
满足条件的情况只有:a=2,b=1或a=4,b=2,a=6,b=3三种情况,
∴直线与圆相切的概率P=
=
故选:B
将得到的点数分别记a,b,则事件总数为6×6=36.
∵直线ax-bx=0与圆x2+(y-5)2=5相切的充要条件是
| 5b | ||
|
| 5 |
即a2=4b2,即a=2b
∵a、b∈{1,2,3,4,5,6}
满足条件的情况只有:a=2,b=1或a=4,b=2,a=6,b=3三种情况,
∴直线与圆相切的概率P=
| 3 |
| 36 |
| 1 |
| 12 |
故选:B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
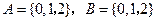 ,分别从集合
,分别从集合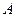 和
和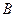 中随机取一个数
中随机取一个数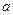 和
和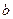 ,确定平面上的一个点
,确定平面上的一个点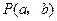 ,记“点
,记“点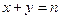 上”
上”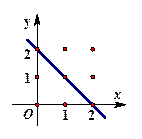
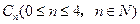 ,若事件
,若事件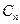 的概率最大,
的概率最大,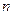 的可能值为( )
的可能值为( )


 与曲线
与曲线 恰有两个不同的交点,记k的所有可能取值构成集合A;P(x,y)是椭圆
恰有两个不同的交点,记k的所有可能取值构成集合A;P(x,y)是椭圆 上一动点,
上一动点, 与点P关于直线y=x+1对称,记
与点P关于直线y=x+1对称,记 的所有可能取值构成集合B,若随机的从集合A,B中分别抽出一个元素
的所有可能取值构成集合B,若随机的从集合A,B中分别抽出一个元素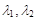 ,则
,则 的概率是___________
的概率是___________