题目内容
14.已知△ABC中,∠ABC=90°,AB=1.AC=2,若△ABC内部的一点P满足$\frac{{S}_{△PAB}}{PA•PB}$=$\frac{{S}_{△PBC}}{PB•PC}=\frac{{S}_{△PAC}}{PA•PC}$,则PA+PB+PC的值为$\sqrt{7}$.分析 由三角形的面积公式可得∠APB=∠BPC=∠APC=120°,以AC为底边向三角形ABC外作正三角形ACQ,可得PA+PB+PC=BQ,由余弦定理可得.
解答 解:由三角形的面积公式可得S△PAB=$\frac{1}{2}$•PA•PBsin∠APB,
S△PBC=$\frac{1}{2}$•PB•PCsin∠BPC,S△PAC=$\frac{1}{2}$•PA•PCsin∠APC,
∴已知式子可化为sin∠APB=sin∠BPC=sin∠APC,
由几何关系可得∠APB=∠BPC=∠APC=120°,
以AC为底边向三角形ABC外作正三角形ACQ,
由题意可得∠ABC=90°,AB=1,AC=2,
∴∠BAC=60°,∠BAQ=120°,
故PA+PB+PC=BQ=$\sqrt{{1}^{2}+{2}^{2}-2×1×2×cos120°}$=$\sqrt{7}$
故答案为:$\sqrt{7}$
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式和余弦定理的应用,属中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
6.用更相减损术得111与148的最大公约数为( )
| A. | 1 | B. | 17 | C. | 23 | D. | 37 |

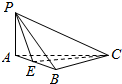 如图,三棱锥P-ABC中,△PAB是正三角形,E是AB的中点,AB⊥BC,平面PAB⊥平面ABC.若AB=2,BC=$\sqrt{2}$,则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$.
如图,三棱锥P-ABC中,△PAB是正三角形,E是AB的中点,AB⊥BC,平面PAB⊥平面ABC.若AB=2,BC=$\sqrt{2}$,则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$.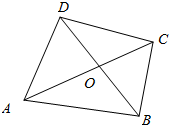 如图所示,在四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,对角线AC与BD交于点O,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
如图所示,在四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,对角线AC与BD交于点O,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.