题目内容
19.已知函数${f_n}(x)=a{x^n}+bx+c(a,b,c∈R)$(1)若f1(x)=3x+1,f2(x)为偶函数,求a,b,c的值;
(2)若对任意实数x,不等式$2x≤{f_2}(x)≤\frac{1}{2}{(x+1)^2}$恒成立,求f2(-1)的取值范围.
分析 (1)由f1(x)=3x+1,f2(x)=ax2+bx+c为偶函数,运用偶函数的定义和恒等式的知识即可得到a,b,c;
(2)先令x=1,可得f2(1)=2,即a+b+c=2,再由不等式恒成立,结合二次函数的判别式小于等于0,及配方思想,可得a的范围,进而得到f2(-1)=4a-2,可得范围.
解答 解:(1)f1(x)=3x+1,f2(x)=ax2+bx+c为偶函数,
可得a+b=3,b=0,c=1,
解得a=3,b=0,c=1;
(2)可令x=1,即有2≤f2(1)≤2,
则f2(1)=2,即a+b+c=2,
由2x≤f2(x)恒成立,即为ax2+(b-2)x+c≥0,
可得a>0,且(b-2)2-4ac≤0,
即有(a+c)2-4ac≤0,即有(a-c)2≤0,
则a=c成立,
即有b=2-2a,又f2(x)-$\frac{1}{2}$(x+1)2=ax2+(2-2a)x+a-$\frac{1}{2}$(x+1)2=(a-$\frac{1}{2}$)(x-1)2,
对任意的x∈R,都有f2(x)≤$\frac{1}{2}$(x+1)2,即有0<a≤$\frac{1}{2}$,
故f2(-1)=a-b+c=4a-2的取值范围是(-2,0].
点评 本题考查函数的性质和应用,考查不等式恒成立问题的解法,注意运用判别式和配方思想,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.四棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为( )
| A. | 6cm2 | B. | $\frac{{3\sqrt{5}}}{4}$cm2 | C. | $\frac{2}{3}$$\sqrt{3}$cm2 | D. | 3$\sqrt{5}$cm2 |
4. 运行如图的程序,若x=1,则输出的y等于( )
运行如图的程序,若x=1,则输出的y等于( )
 运行如图的程序,若x=1,则输出的y等于( )
运行如图的程序,若x=1,则输出的y等于( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
11.若曲线x2-4x+y2-2y+4=0(y≥1)与直线y=k(x+1)有2个公共点,则k的取值范围是( )
| A. | (0,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{3}{4}$] | C. | [$\frac{1}{2}$,$\frac{3}{4}$) | D. | [$\frac{1}{4}$,1) |
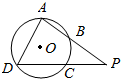 如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.
如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.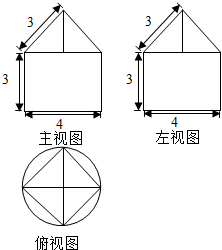 一个空间几何体的三视图如图所示,根据图中数据:
一个空间几何体的三视图如图所示,根据图中数据: