题目内容
3．
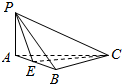如图，三棱锥P-ABC中，△PAB是正三角形，E是AB的中点，AB⊥BC，平面PAB⊥平面ABC．若AB=2，BC=$\sqrt{2}$，则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$．
分析 利用VA-PEC=VP-AEC，即可求出点A到平面PEC的距离．
解答 解：设点A到平面PEC的距离是h，则
由题意，PE⊥平面ABC，PE=$\sqrt{3}$，EC=$\sqrt{3}$，
∴S△PEC=$\frac{1}{2}•\sqrt{3}•\sqrt{3}$=$\frac{3}{2}$，
∵VP-AEC=$\frac{1}{3}•\frac{1}{2}•1•\sqrt{2}•\sqrt{3}$=$\frac{\sqrt{6}}{6}$，
∴VA-PEC=$\frac{1}{3}•\frac{3}{2}•h$=$\frac{\sqrt{6}}{6}$，
∴h=$\frac{\sqrt{6}}{3}$．
故答案为：$\frac{\sqrt{6}}{3}$．
点评 本题考查求点A到平面PEC的距离，考查三棱锥体积的计算，正确求体积是关键．
练习册系列答案
相关题目
11．若曲线x2-4x+y2-2y+4=0（y≥1）与直线y=k（x+1）有2个公共点，则k的取值范围是（ ）
| A． | （0，$\frac{1}{2}$] | B． | （$\frac{1}{4}$，$\frac{3}{4}$] | C． | [$\frac{1}{2}$，$\frac{3}{4}$） | D． | [$\frac{1}{4}$，1） |