题目内容
4．
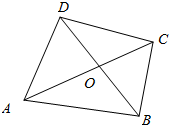如图所示，在四边形ABCD中，$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，对角线AC与BD交于点O，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$．
分析 由题意得$\overrightarrow{AB}$=$\overrightarrow{AO}$+$\overrightarrow{OB}$=-$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{b}$-$\overrightarrow{a}$，由$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$可得四边形ABCD是平行四边形，从而求得$\overrightarrow{AD}$=$\overrightarrow{AO}$+$\overrightarrow{OD}$=-（$\overrightarrow{b}$+$\overrightarrow{a}$）．
解答 解：∵$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，
∴$\overrightarrow{AB}$=$\overrightarrow{AO}$+$\overrightarrow{OB}$=-$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{b}$-$\overrightarrow{a}$，
∵$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，
∴四边形ABCD是平行四边形，
∴$\overrightarrow{OB}$=-$\overrightarrow{OD}$=$\overrightarrow{b}$，
∴$\overrightarrow{AD}$=$\overrightarrow{AO}$+$\overrightarrow{OD}$=-（$\overrightarrow{b}$+$\overrightarrow{a}$）．
点评 本题考查了平面向量的加法及其几何意义的应用．
