题目内容
(16分)已知数列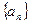 是等差数列,
是等差数列,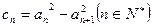
(1)判断数列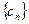 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果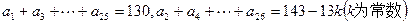 ,试写出数列
,试写出数列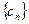 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列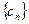 得前n项和为
得前n项和为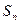 ,问是否存在这样的实数
,问是否存在这样的实数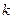 ,使
,使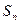 当且仅当
当且仅当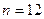 时取得最大值。若存在,求出
时取得最大值。若存在,求出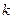 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
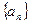 是等差数列,
是等差数列,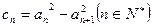
(1)判断数列
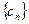 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;(2)如果
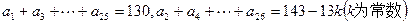 ,试写出数列
,试写出数列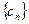 的通项公式;
的通项公式;(3)在(2)的条件下,若数列
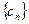 得前n项和为
得前n项和为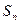 ,问是否存在这样的实数
,问是否存在这样的实数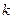 ,使
,使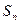 当且仅当
当且仅当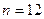 时取得最大值。若存在,求出
时取得最大值。若存在,求出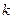 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。(1)数列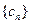 是以
是以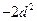 为公差的等差数列
为公差的等差数列
(2)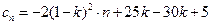
(3)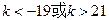
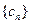 是以
是以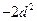 为公差的等差数列
为公差的等差数列(2)
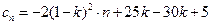
(3)
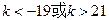
(1)设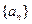 的公差为
的公差为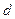 ,则
,则
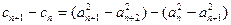
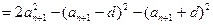

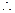 数列
数列 是以
是以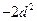 为公差的等差数列…………4分
为公差的等差数列…………4分
(2)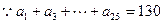

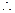 两式相减:
两式相减: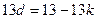
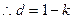 …………6分
…………6分
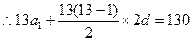
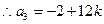 …………8分
…………8分
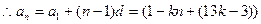
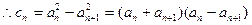
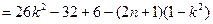
 …………10分
…………10分
(3)因为当且仅当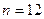 时
时 最大
最大
 …………12分
…………12分
即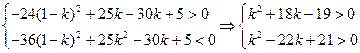
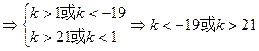 …………15分
…………15分
 的公差为
的公差为 ,则
,则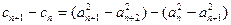
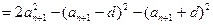

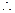 数列
数列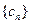 是以
是以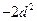 为公差的等差数列…………4分
为公差的等差数列…………4分(2)
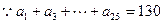

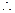 两式相减:
两式相减: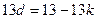
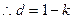 …………6分
…………6分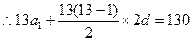
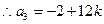 …………8分
…………8分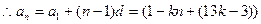
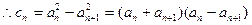
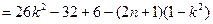
 …………10分
…………10分(3)因为当且仅当
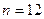 时
时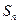 最大
最大 …………12分
…………12分即
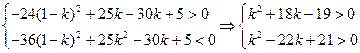
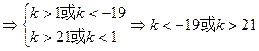 …………15分
…………15分
练习册系列答案
相关题目
 12分)
12分)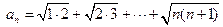 (
( ),比较
),比较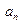 、
、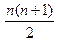 、
、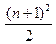 的大小,并证明你的结论
的大小,并证明你的结论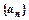 中,
中,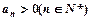 ,公比
,公比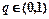 ,且
,且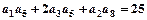 ,又
,又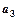 与
与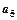 的等比中项为
的等比中项为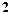 ,
,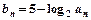 ,数列
,数列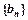 的前
的前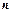 项和为
项和为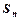 ,求数列
,求数列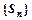 的通项公式
的通项公式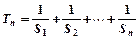 ,求
,求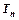
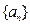 中,若
中,若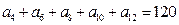 ,则
,则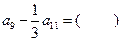
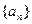 ,
,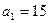 ,
,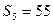 ,则过点
,则过点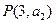 ,
,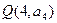 的直线的斜率为 ( )
的直线的斜率为 ( )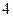
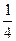
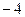
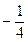
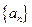 中,
中,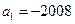 ,其前
,其前
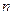 项的和为
项的和为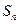 .若
.若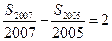 ,则
,则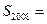 ( )
( )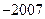
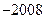
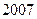
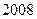
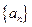 共有
共有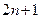 项,其中奇数项之和为319,偶数项
项,其中奇数项之和为319,偶数项 之和为290,则其中间项为 .
之和为290,则其中间项为 .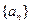 满足
满足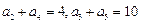 ,则它的前10
,则它的前10 项和
项和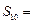 ( )
( ) 
