题目内容
已知不等式组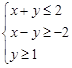 表示的平面区域为
表示的平面区域为 ,若
,若 是区域
是区域 上一点,
上一点,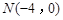 ,则
,则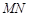 斜率的取值范围是 .
斜率的取值范围是 .
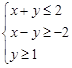 表示的平面区域为
表示的平面区域为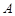 ,若
,若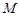 是区域
是区域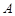 上一点,
上一点,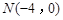 ,则
,则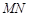 斜率的取值范围是 .
斜率的取值范围是 .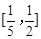
试题分析:根据题意可知,不等式组
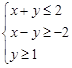 表示的平面区域为
表示的平面区域为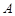 ,即为三角形区域,边界点为(1,1)(0,2)
,即为三角形区域,边界点为(1,1)(0,2)(-1,1),由于
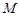 是区域
是区域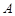 上一点,且
上一点,且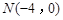 ,是定点,那么根据斜率的几何意义,可知连接边界点与点N的连线中,斜率的最小值和最大值分别是
,是定点,那么根据斜率的几何意义,可知连接边界点与点N的连线中,斜率的最小值和最大值分别是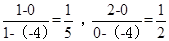 ,故可知答案为
,故可知答案为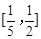 。
。点评:解决该试题的关键是表示出不等式的区域,运用斜率的几何意义,来结合倾斜角与斜率的关系来求解得到结论,属于基础题。

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
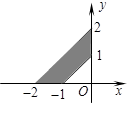
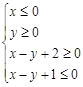
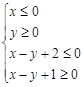

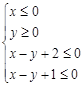
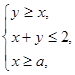 且z的最大值是最小值的4倍,则a的值是 .
且z的最大值是最小值的4倍,则a的值是 .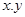 满足不等式组
满足不等式组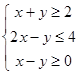 , 则
, 则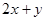 的最小值是 。
的最小值是 。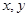 满足不等式
满足不等式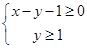 ,则
,则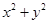 的最小值为 .
的最小值为 .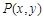 在圆
在圆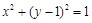 上运动,则
上运动,则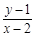 的最大值与最小值为( )
的最大值与最小值为( )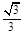 ,
,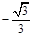
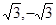
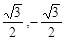
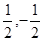
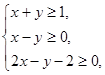 则目标函数z=2x+y的最小值为( )
则目标函数z=2x+y的最小值为( )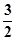
 。若
。若 ,则
,则 的最大值为
的最大值为