题目内容
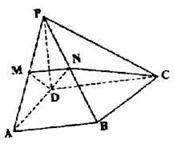
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.
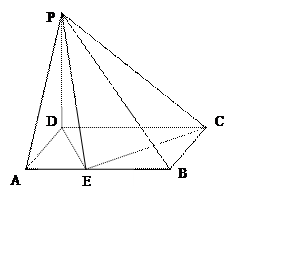 已知PD=
已知PD=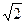 ,CD=2,AE=
,CD=2,AE=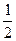 ,
,
(1)求证:平面PED⊥平面PEC
(2)求二面角E-PC-D的大小。
 已知PD=
已知PD=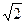 ,CD=2,AE=
,CD=2,AE=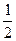 ,
,(1)求证:平面PED⊥平面PEC
(2)求二面角E-PC-D的大小。
(Ⅰ)见解析 (Ⅱ)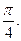
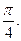
.证明:(Ⅰ)∵PD⊥底面ABCD ∴PD⊥EC
又∵PE⊥EC PD∩PE="P" ∴EC⊥平面PED
又∵EC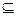 平面PEC ∴平面PED⊥平面PEC …………6分
平面PEC ∴平面PED⊥平面PEC …………6分
(Ⅱ)以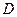 为原点,
为原点,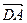 、
、 、
、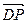 分别为
分别为
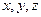 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由已知可得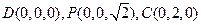 ,E(x,
,E(x,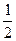 ,0)
,0)
∵PE⊥EC ∴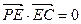 ∴E(
∴E(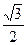 ,
,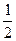 ,0)
,0)
可得平面PEC的一个法向量为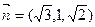
又∵平面PED的一个法向量为 …………10分
…………10分
故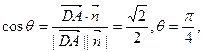 即二面角
即二面角 的大小为
的大小为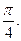 …………12分
…………12分
又∵PE⊥EC PD∩PE="P" ∴EC⊥平面PED
又∵EC
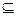 平面PEC ∴平面PED⊥平面PEC …………6分
平面PEC ∴平面PED⊥平面PEC …………6分(Ⅱ)以
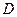 为原点,
为原点,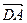 、
、 、
、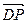 分别为
分别为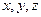 轴建立空间直角坐标系.
轴建立空间直角坐标系.由已知可得
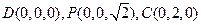 ,E(x,
,E(x,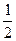 ,0)
,0)∵PE⊥EC ∴
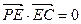 ∴E(
∴E(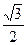 ,
,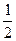 ,0)
,0)可得平面PEC的一个法向量为
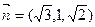
又∵平面PED的一个法向量为
 …………10分
…………10分故
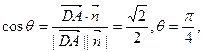 即二面角
即二面角 的大小为
的大小为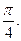 …………12分
…………12分
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
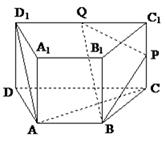
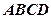 中,
中,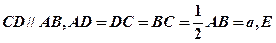 是
是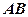 的中点,将
的中点,将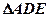 沿
沿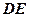 折起,使点
折起,使点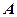 到点
到点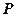 的位置,使二面角
的位置,使二面角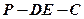 的大小为
的大小为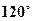
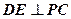 ;
;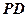 与平面
与平面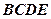 所成角的正弦值
所成角的正弦值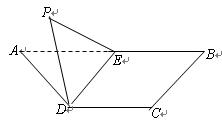
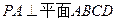 ,底面ABCD是直角梯形,
,底面ABCD是直角梯形, ,且AB∥CD,
,且AB∥CD,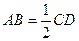 , 点F为线段PC的中点,
, 点F为线段PC的中点, 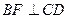 。
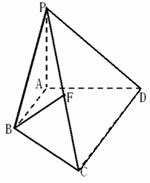
。 
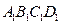 中,AB=2,
中,AB=2,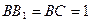 ,E为
,E为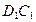 的中点,连结ED,EC,EB和DB,
的中点,连结ED,EC,EB和DB,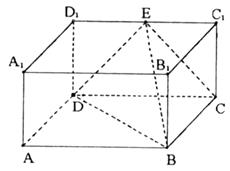
 BCD的三条高线的交点;
BCD的三条高线的交点;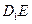 ⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).
⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).
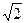 ,PB⊥PD.
,PB⊥PD.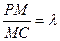 ,问
,问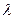 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.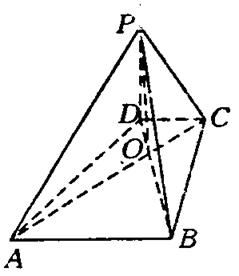
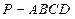 中,
中,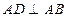 ,
,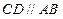 ,
,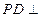 底面
底面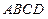 ,
, 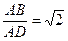 ,直线
,直线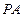 与底面
与底面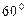 角,点
角,点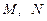 分别是
分别是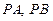 的中点.
的中点.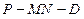 的大小;
的大小;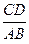 的值为多少时,
的值为多少时,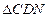 为直角三角形.
为直角三角形.