��Ŀ����
����Ŀ����ͼ����Ӱ��������ij��A����������ǰ��B����һ�����������������O�����Ǻ������ײ�B�ĸ��Ǿ�Ϊ![]() ����֪��Ӱ�����ߵ�����ԼΪ
����֪��Ӱ�����ߵ�����ԼΪ![]() �ף����۾�S�����ľ���SA��
�ף����۾�S�����ľ���SA��![]() �״�������
�״�������
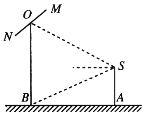
��1������Ӱ�����ߵ�������ˮƽ����AB�������ĸ߶�OB��
��2�������Ķ�����һ��Ϊ2�IJʸ�MN����MN�����е�O����Ӱ���������������ڵ�ƽ������ת���ڲʸ�ת��������ʱ�̣���Ӱ�����߹۲�ʸ�MN���ӽ�![]() ����Ϊ
����Ϊ![]() ���Ƿ�������ֵ�������ڣ������
���Ƿ�������ֵ�������ڣ������![]() ȡ���ֵʱ
ȡ���ֵʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1) ABΪ3�� OBΪ2![]() �� (2) ���ӽ���MSNȡ���ֵʱ,cos��=
�� (2) ���ӽ���MSNȡ���ֵʱ,cos��=![]() .
.
��������
(1)��ͼ,��SC��OB��C,
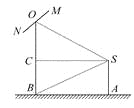
��������CSB=30��,��ASB=60��.
��SA=![]() ,����Rt��SAB��,�����AB=
,����Rt��SAB��,�����AB=![]() =3,
=3,
����Ӱ�����ߵ�������ˮƽ����ABΪ3��.
��Rt��SCO��,SC=3,��CSO=30��,OC=SC��tan 30��=![]() ,
,
��BC=SA=![]() ,��OB=2
,��OB=2![]() ,�������ĸ߶�OBΪ2
,�������ĸ߶�OBΪ2![]() ��.
��.
(2)����һ:��ͼ,��OΪԭ��,��ˮƽ��������Ϊx����������ƽ��ֱ������ϵ,����SM,SN,
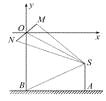
��M(cos��,sin��),����[0,2��),
��N(-cos��,-sin��),��(1)֪S(3,-![]() ).
).
��![]() =(cos��-3,sin��+
=(cos��-3,sin��+![]() ),
),
![]() =(-cos��-3,-sin��+
=(-cos��-3,-sin��+![]() ),
),
��![]() ��
��![]() =(cos��-3)��(-cos��-3)+(sin��+
=(cos��-3)��(-cos��-3)+(sin��+![]() )��(-sin��+
)��(-sin��+![]() )=11.
)=11.
|![]() |��|
|��|![]() |=
|=![]() ��
��
![]()
=![]() ��
��
![]()
=![]()
=![]() .
.
������[0,2��)֪|![]() |��|
|��|![]() |��[11,13].
|��[11,13].
����cos��MSN=![]() ��[
��[![]() ,1],��֪��MSNΪ���,
,1],��֪��MSNΪ���,
�ʵ��ӽ���MSNȡ���ֵʱ,cos��=![]() .
.
������:��cos��MOS=-cos��NOS,
��![]() =-
=-![]()
���ǵ�SM2+SN2=26�Ӷ�
cos��=![]() ��
��![]() =
=![]() .
.
����MSN���,
�ʵ��ӽ���MSNȡ���ֵʱ,cos��=![]() .
.

����Ŀ�������ź�ĸ�����´�2012��10��5����ʼ���У�ͨ���г����飬�õ��ü�����ÿ![]() ö���г���
ö���г���![]() ����λ��Ԫ��������ʱ��
����λ��Ԫ��������ʱ��![]() ����λ���죩���������£�
����λ���죩���������£�
����ʱ�� |
|
|
|
��� |
|
|
|
��1�������ϱ����ݣ������к�����ѡȡһ��ǡ���ĺ������������ź�ĸ�����µ��г���![]() ������ʱ��
������ʱ��![]() �ı仯��ϵ����
�ı仯��ϵ����![]() ����
����![]() ����
����![]() ��
��
��2��������ѡȡ�ĺ������������ź�ĸ�������г������ʱ��������������͵ļ۸�
��3������ѡȡ�ĺ���Ϊ![]() ����������ʵ��
����������ʵ��![]() ������
������![]() �ķ���
�ķ���![]() ���и�����ʵ��������
���и�����ʵ��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.