题目内容
【题目】已知函数f(x)=|2x﹣1|,当a<b<c时,f(a)>f(c)>f(b),那么正确的结论是( )
A.2a>2b
B.2a>2c
C.2﹣a<2c
D.2a+2c<2
【答案】D
【解析】∵函数f(x)=|2x﹣1|,
∴f(x)=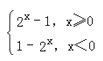 .
.
画出函数图象如下图所示: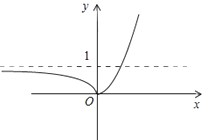
可知:函数f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增.
当0≤a<b<c时,f(x)在区间(0,+∞)上单调递增,不满足f(a)>f(b)>f(c),因此必有a<0.
当a<0<c时,1﹣2a>2c﹣1,化为2a+2c<2;
当a<b<c≤0时,f(x)在区间(﹣∞,0]上单调递减.
∴1>1﹣2a>1﹣2c≥0,
∴2c≤1,2a<1,
∴2a+2c<2.
综上可知:D一定正确.
故选:D.
函数f(x)=|2x﹣1|,可得f(x)=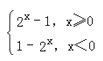 . 画出函数图象.利用函数图象的单调性和已知条件可得:当0≤a<b<c时,不满足f(a)>f(b)>f(c),因此必有a<0.当a<0<c时,1﹣2a>2c﹣1,化为2a+2c<2;当a<b<c≤0时,f(x)在区间(﹣∞,0]上也满足2a+2c<2.
. 画出函数图象.利用函数图象的单调性和已知条件可得:当0≤a<b<c时,不满足f(a)>f(b)>f(c),因此必有a<0.当a<0<c时,1﹣2a>2c﹣1,化为2a+2c<2;当a<b<c≤0时,f(x)在区间(﹣∞,0]上也满足2a+2c<2.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系:①
的变化关系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;
(3)设你选取的函数为![]() ,若对任意实数
,若对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 恒有个想异实数根,求
恒有个想异实数根,求![]() 的取值范围.
的取值范围.