题目内容
【题目】已知函数![]() ,设关于
,设关于![]() 的方程
的方程![]() 有
有![]() 个不同的实数解,则
个不同的实数解,则![]() 的所有可能的值为( )
的所有可能的值为( )
A. 3 B. 1或3 C. 4或6 D. 3或4或6
【答案】A
【解析】f′(x)=(x﹣1)(x+3)ex,所以f(x)在(﹣∞,﹣3)和(1,+∞)上单调递增,(﹣3,1)上单调递减,又当x→﹣∞时f(x)→0,x→+∞时f(x)→+∞,故f(x)的图象大致为:
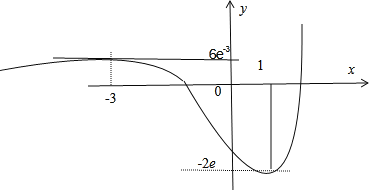
令f(x)=t,则方程![]() 必有两个实根t1,t2(t1<t2)且
必有两个实根t1,t2(t1<t2)且![]() ,
,
当t1=﹣2e时恰有![]() ,此时f(x)=t1有1个根,f(x)=t2有2个根;
,此时f(x)=t1有1个根,f(x)=t2有2个根;
当t1<﹣2e时必有![]() ,此时f(x)=t1无根,f(x)=t2有3个根;
,此时f(x)=t1无根,f(x)=t2有3个根;
当﹣2e<t1<0时必有![]() ,此时f(x)=t1有2个根,f(x)=t2有1个根;
,此时f(x)=t1有2个根,f(x)=t2有1个根;
综上,对任意m∈R,方程均有3个根.
故选:A.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目