题目内容
在等比数列{an}中,an>0(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,又a3与a5的等比中项为2.(1)求数列{an}的通项公式;
(2)设bn=log2an,数列{bn}的前n项和为Sn,求数列{Sn}的通项公式;
(3)是否存在k∈N*,使得
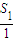 +
+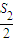 +…+
+…+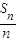 <k对任意n∈N*恒成立,若存在,求出k的最小值,若不存在,请说明理由.
<k对任意n∈N*恒成立,若存在,求出k的最小值,若不存在,请说明理由.
【答案】分析:(1)根据等比数列的性质可知a1a5=a32,a2a8=a52化简a1a5+2a3a5+a2a8=25得到a3+a5=5,又因为a3与a5的等比中项为2,联立求得a3与a5的值,求出公比和首项即可得到数列的通项公式;
(2)把an代入到bn=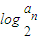 中得到bn的通项公式,即可得到前n项和的通项sn;
中得到bn的通项公式,即可得到前n项和的通项sn;
(3)把sn代入得到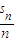 ,讨论求出
,讨论求出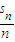 各项和的最大值,即可求出k的取值范围.
各项和的最大值,即可求出k的取值范围.
解答:解:(1)∵a1a5+2a3a5+a2a8=25,
∴a32+2a3a5+a52=25,
∴(a3+a5)2=25,
又an>0,∴a3+a5=5,
又a3与a5的等比中项为2,
∴a3a5=4.
而q∈(0,1),
∴a3>a5,∴a3=4,a5=1,
∴q= ,a1=16,∴an=16×(
,a1=16,∴an=16×( )n-1=25-n.
)n-1=25-n.
(2)∵bn=log2an=5-n,∴bn+1-bn=-1,
b1=log2a1=log216=log224=4,
∴{bn}是以b1=4为首项,-1为公差的等差数列,
∴Sn= .
.
(3)由(2)知Sn=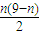 ,∴
,∴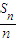 =
=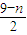 .
.
当n≤8时,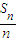 >0;当n=9时,
>0;当n=9时,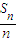 =0;
=0;
当n>9时,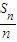 <0.
<0.
∴当n=8或9时,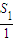 +
+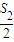 +
+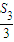 ++
++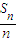 =18最大.
=18最大.
故存在k∈N*,使得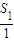 +
+ ++
++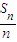 <k对任意n∈N*恒成立,k的最小值为19.
<k对任意n∈N*恒成立,k的最小值为19.
点评:考查学生灵活运用等比数列性质的能力,掌握等比数列的通项公式,会进行数列的求和,理解函数恒成立时所取的条件.
(2)把an代入到bn=
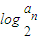 中得到bn的通项公式,即可得到前n项和的通项sn;
中得到bn的通项公式,即可得到前n项和的通项sn;(3)把sn代入得到
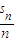 ,讨论求出
,讨论求出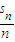 各项和的最大值,即可求出k的取值范围.
各项和的最大值,即可求出k的取值范围.解答:解:(1)∵a1a5+2a3a5+a2a8=25,
∴a32+2a3a5+a52=25,
∴(a3+a5)2=25,
又an>0,∴a3+a5=5,
又a3与a5的等比中项为2,
∴a3a5=4.
而q∈(0,1),
∴a3>a5,∴a3=4,a5=1,
∴q=
 ,a1=16,∴an=16×(
,a1=16,∴an=16×( )n-1=25-n.
)n-1=25-n.(2)∵bn=log2an=5-n,∴bn+1-bn=-1,
b1=log2a1=log216=log224=4,
∴{bn}是以b1=4为首项,-1为公差的等差数列,
∴Sn=
 .
.(3)由(2)知Sn=
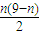 ,∴
,∴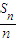 =
=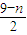 .
.当n≤8时,
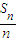 >0;当n=9时,
>0;当n=9时,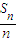 =0;
=0;当n>9时,
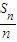 <0.
<0.∴当n=8或9时,
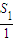 +
+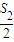 +
+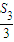 ++
++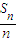 =18最大.
=18最大.故存在k∈N*,使得
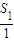 +
+ ++
++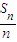 <k对任意n∈N*恒成立,k的最小值为19.
<k对任意n∈N*恒成立,k的最小值为19.点评:考查学生灵活运用等比数列性质的能力,掌握等比数列的通项公式,会进行数列的求和,理解函数恒成立时所取的条件.

练习册系列答案
相关题目
在等比数列{an}中,若a1=1,公比q=2,则a12+a22+…+an2=( )
| A、(2n-1)2 | ||
B、
| ||
| C、4n-1 | ||
D、
|