题目内容
(本小题满分14分)
二次函数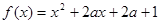 .
.
(1)若对任意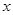
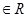 有
有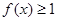 恒成立,求实数
恒成立,求实数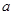 的取值范围;
的取值范围;
(2)讨论函数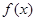 在区间
在区间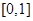 上的单调性;
上的单调性;
(3)若对任意的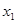 ,
,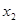
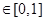 有
有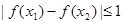 恒成立,求实数
恒成立,求实数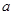 的取值范围.
的取值范围.
二次函数
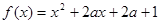 .
.(1)若对任意
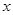
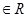 有
有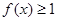 恒成立,求实数
恒成立,求实数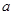 的取值范围;
的取值范围;(2)讨论函数
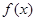 在区间
在区间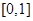 上的单调性;
上的单调性;(3)若对任意的
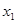 ,
,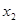
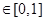 有
有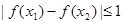 恒成立,求实数
恒成立,求实数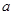 的取值范围.
的取值范围.(1) ;(2)①当
;(2)①当 即
即 时,
时,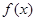 在区间
在区间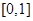 上单调递增;
上单调递增;
②当 即
即 时,
时,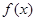 在区间
在区间 上单调递减,在区间
上单调递减,在区间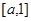 上单调递增;
上单调递增;
③当 即
即 时,
时,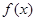 在区间
在区间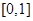 上单调递增.(3)
上单调递增.(3) 。
。
 ;(2)①当
;(2)①当 即
即 时,
时,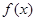 在区间
在区间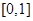 上单调递增;
上单调递增;②当
 即
即 时,
时,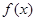 在区间
在区间 上单调递减,在区间
上单调递减,在区间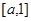 上单调递增;
上单调递增;③当
 即
即 时,
时,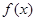 在区间
在区间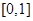 上单调递增.(3)
上单调递增.(3) 。
。试题分析:(1)
 对任意
对任意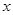
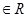 恒成立 …………1分
恒成立 …………1分 …………2分 解得
…………2分 解得

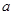 的范围是
的范围是 …………3分
…………3分(2)
 ,其图象是开口向上的抛物线,对称轴方程为
,其图象是开口向上的抛物线,对称轴方程为 ,……4分
,……4分讨论:①当
 即
即 时,
时,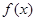 在区间
在区间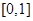 上单调递增;
上单调递增;②当
 即
即 时,
时,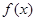 在区间
在区间 上单调递减,在区间
上单调递减,在区间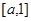 上单调递增;
上单调递增;③当
 即
即 时,
时,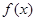 在区间
在区间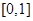 上单调递增. ……………8分
上单调递增. ……………8分(3)由题知,
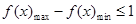 ………9分
………9分 ,
, ,
, 由(2),
由(2), 或
或 或
或 ………………12分
………………12分解得
 ……………14分
……………14分点评:若

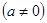 恒成立
恒成立
 ;若
;若
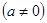 恒成立
恒成立
 。此题中没有限制二次项系数不为零,所以不要忘记讨论。
。此题中没有限制二次项系数不为零,所以不要忘记讨论。
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
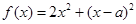 .
.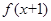 为偶函数,求
为偶函数,求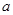 的值;
的值;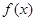 在
在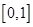 上有最小值9,求
上有最小值9,求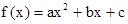 满足:
满足: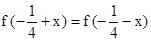 ,且
,且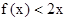 的
的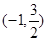
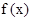 的解析式;
的解析式;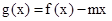
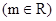 ,若
,若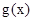 在
在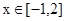 上的最小值为-4,求
上的最小值为-4,求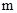 的值.
的值.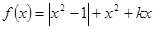 ,
,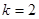 ,求方程
,求方程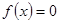 的解;
的解;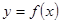 在
在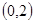 上有两个零点,求
上有两个零点,求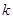 的取值范围.
的取值范围. 的增区间是( )
的增区间是( ) ,2]
,2] )
)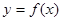 的图象过点(0,—3),且
的图象过点(0,—3),且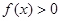 的解集(1,3)。
的解集(1,3)。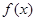 的解析式;
的解析式;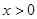 时,恒有
时,恒有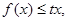 求实数t的取值范围。
求实数t的取值范围。 ,则
,则 的解集为
的解集为



 的图象如图所示,
的图象如图所示, 是图象上的一点,且
是图象上的一点,且 ,则
,则 的值为:
的值为: 

