题目内容
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.
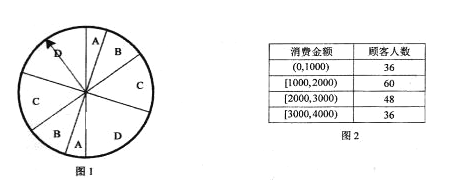
(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
【答案】(1)详见解析(2)![]()
【解析】
(1)分别计算出X=50,100,150,200对应的概率,计算期望,即可。(2)结合古典概型,计算出![]() ,结合
,结合![]() ,即可。
,即可。
解:(1)设标有A,B,C,D的扇形区域的圆心角分别为![]()
由题意知:![]()
所以顾客抽奖一次,获得奖金X可能取值为50,100,150,200,所对应的概率分别为 ![]()
所以X的分布列为
X | 50 | 100 | 150 | 200 |
P |
|
|
|
|
期望![]()
(2)由已知得:
1消费金额位于![]() 内的顾客,获奖金额一定高于100元,
内的顾客,获奖金额一定高于100元,
2消费金额位于![]() 内的顾客获奖金额为0元,
内的顾客获奖金额为0元,
3消费金额位于![]() 内的顾客获奖金额可能为50,100,150,200元
内的顾客获奖金额可能为50,100,150,200元
分层抽样得 ![]() 内抽到的顾客代表人数为
内抽到的顾客代表人数为![]() 人,
人,
则获得奖金总数不足100元的剩余4位顾客代表必然获得奖金数为50元.
设获奖金额为0元的三位顾客代表为![]() ,获奖金额为50元的四位顾客代表为
,获奖金额为50元的四位顾客代表为 ![]()
事件 ![]() “从这7位顾客代表中随机选取两位的奖金总数仍不足100元”
“从这7位顾客代表中随机选取两位的奖金总数仍不足100元”
![]() “从这7位顾客代表中随机选取两位的奖金总数等于100元”
“从这7位顾客代表中随机选取两位的奖金总数等于100元”
从这7位顾客代表中随机选取两位的基本事件空间为:
![]() 共有21个基本事件;
共有21个基本事件;
![]() 共有6个基本事件。
共有6个基本事件。
![]()
从这7位顾客代表中随机选取两位,他们的奖金总数仍不足100元的概率为![]()

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷,某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)求出表格中![]() 的值,并根据表中的数据,判断能否在犯错误的概率不超过
的值,并根据表中的数据,判断能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.
参考公式: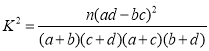 .
.
|
|
|
|
|
|
|
|
|
|