题目内容
【题目】已知抛物线
：
经过点
，直线
分别与抛物线交于点
，若直线的斜率之和为零，则直线
的斜率为_________。
【答案】-2
【解析】
将P（1，4）代入y2＝2px可解得p＝8，得抛物线方程为y2＝16x，在设出直线PA的方程并与抛物线方程联立解得A的坐标，同理解得B的坐标，最后用斜率公式可求得AB的斜率为定值﹣2．
因为抛物线C：y2＝2px经过点P（1，4），∴p＝8，∴抛物线C：y2＝16x，设直线PA：y﹣4＝k（x﹣1），并代入y2＝16x消去x并整理得k2x2+（8k﹣2k2﹣16）xx+（4﹣k）2＝0，
设A（x1，y1），B（x2，y2）依题意知1和x1是以上一元二次方程的两个根，∴1x1＝
，∴x1＝
，∴y1＝4﹣k+kx1＝4﹣k+k＝
﹣4，同理得x2＝
，y2＝﹣﹣4，所以直线AB的斜率为：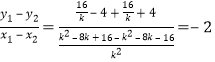
．
故答案为：﹣2
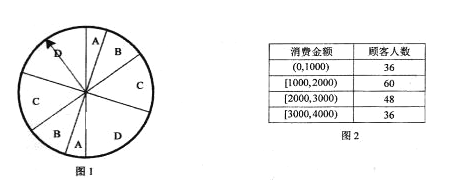
黄冈冠军课课练系列答案
【题目】随着国家二孩政策的全面放开，为了调查一线城市和非一线城市的二孩生育意愿，某机构用简单随机抽样方法从不同地区调查了
位育龄妇女，结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表：
|
|
|
|
|
|
|
|
由
算得，
参照附表，得到的正确结论是（ ）
A. 在犯错误的概率不超过
的前提下，认为“生育意愿与城市级别有关”
B. 有
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过的前提下，认为“生育意愿与城市级别无关”
D. 有以上的把握认为“生育意愿与城市级别无关”
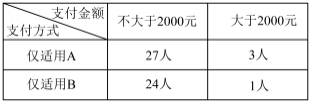
【题目】改革开放以来，人们的支付方式发生了巨大转变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月A，B两种移动支付方式的使用情况，从全校所有的1000名学生中随机抽取了100人，发现样本中A，B两种支付方式都不使用的有5人，样本中仅使用A和仅使用B的学生的支付金额分布情况如下：
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
（Ⅰ）估计该校学生中上个月A，B两种支付方式都使用的人数；
（Ⅱ）从样本仅使用B的学生中随机抽取1人，求该学生上个月支付金额大于2000元的概率；
（Ⅲ）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用B的学生中随机抽查1人，发现他本月的支付金额大于2000元．结合（Ⅱ）的结果，能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化？说明理由．
