题目内容
4.已知数列{an}是等差数列,Sn是数列{an}的前n项和,且a1=-1,S3=3(1)求数列{an}的通项公式
(2)设bn=$\frac{2}{n({a}_{n}+5)}$(n∈N*),求数列{bn}的前n和Tn.
分析 (1)根据等差数列的通项公式以及前n项和公式建立条件关系,求出公差d,即可求数列{an}的通项公式.
(2)求出bn=$\frac{2}{n({a}_{n}+5)}$的表达式,利用裂项法进行求和.
解答 解:(1)设公差为d,
∵a1=-1,S3=3,
∴3a1+$\frac{3×2}{2}d=3$,解得d=2,
则数列{an}的通项公式an=-1+2(n-1)=2n-3.
(2)bn=$\frac{2}{n({a}_{n}+5)}$=$\frac{2}{n(2n-3+5)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
则数列{bn}的前n和Tn=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+$$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{1+n}$.
点评 本题主要考查数列通项公式的求解,以及利用裂项法进行求和,比较基础.

练习册系列答案
相关题目
19.运行如图所示的程序框图,输出的所有实数对(x,y)所对应的点都在函数( )
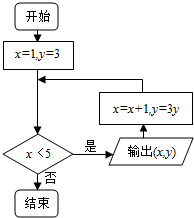

| A. | y=x+2图象上 | B. | y=3x图象上 | C. | y=3x的图象上 | D. | y=3x3图象上 |
9.下列抽样问题中最适合用分层抽样法进行抽样的是( )
| A. | 从12名学生中随机抽泣8人参加活动 | |
| B. | 某单位有210名员工,其中老年员工20人,中年员工40人,青年员工150人,为了解情况,要从中抽取一个容量为21的样本 | |
| C. | 从参加期中考试的1200名高中生随机抽取100人分析作答情况 | |
| D. | 从1200名观众中随机抽取3名幸运观众 |