题目内容
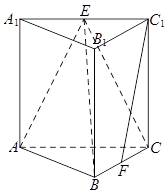
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.


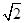
由于在正方体ABCD-A1B1C1D1中,AB=2,∴AC=2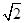 .又E为AD中点,EF∥平面AB1C,EF?平面ADC,平面ADC∩平面AB1C=AC,∴EF∥AC,∴F为DC中点,
.又E为AD中点,EF∥平面AB1C,EF?平面ADC,平面ADC∩平面AB1C=AC,∴EF∥AC,∴F为DC中点,
∴EF=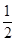 AC=
AC=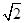 .
.
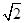 .又E为AD中点,EF∥平面AB1C,EF?平面ADC,平面ADC∩平面AB1C=AC,∴EF∥AC,∴F为DC中点,
.又E为AD中点,EF∥平面AB1C,EF?平面ADC,平面ADC∩平面AB1C=AC,∴EF∥AC,∴F为DC中点,∴EF=
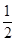 AC=
AC=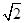 .
.
练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目

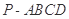 中,
中,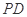 ⊥底面
⊥底面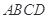 ,底面
,底面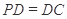 ,
,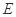 ,
,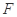 分别是
分别是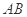 ,
,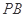 的 中点.
的 中点.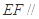 平面
平面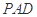 ;
;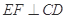 ;
;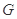 是线段
是线段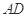 上一动点,试确定
上一动点,试确定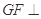 平面
平面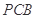 ,并证明你的结论.
,并证明你的结论.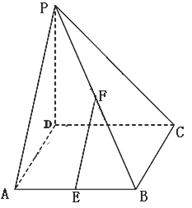
 中,底面
中,底面 是矩形,
是矩形,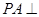 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
;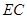 与平面
与平面 所成角的正弦值.
所成角的正弦值.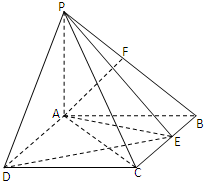
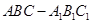 中,侧棱垂直于底面,
中,侧棱垂直于底面,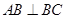 ,
,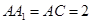 ,
,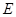 、
、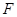 分别为
分别为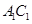 、
、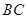 的中点.
的中点.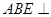 平面
平面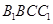 ;
;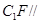 平面
平面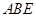 ;
;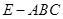 的体积.
的体积.