题目内容
(本小题满分16分)已知函数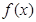 =
=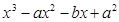 ,
,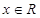 ,
,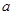 ,
,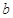 为常数。
为常数。
(1)若函数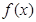 在
在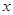 =1处有极值10,求实数
=1处有极值10,求实数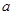 ,
,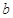 的值;
的值;
(2)若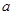 =0,(I)方程
=0,(I)方程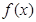 =2在
=2在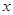 ∈[-4,4]上恰有3个不相等的实数解,求实数
∈[-4,4]上恰有3个不相等的实数解,求实数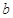 的取值范围;(II)不等式
的取值范围;(II)不等式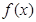 +2
+2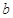 ≥0对
≥0对
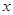 ∈[1,4]恒成立,求实数
∈[1,4]恒成立,求实数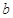 的取值范围。
的取值范围。
解:(1)f’(x)=3x2-2ax-b,
由f(x)在x=1处有极值10,得f’(1)=0,f(1)=10。 (2分)
即3-2a-b=0,1-a-b+a‑2=10,解得a=3,b=-3或a=-4,b=11。 (4分)
经检验,a=3,b=-3不合题意,舍去。
∴a=-4,b=11。 (5分)
(2)(I)由f(x)=2,得f(x)-2=0,令g(x)=f(x)-2=x3-bx-2,则方程g(x)=0在x∈[-4,4]上恰有3个不相等的实数解。 ∵g’(x)=3x2-b,
(ⅰ)若b≤0,则g’(x)≥0恒成立,且函数g(x)不为常函数,∴g(x)在区间[-4,4]上为增函数,不合题意,舍去。 (6分)
(ⅱ)若b>0,则函数g(x)在区间(-∞,-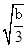 )上为增函数,在区间(-
)上为增函数,在区间(-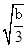 ,
,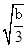 )上为减函数,在区间(
)上为减函数,在区间(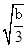 ,+∞)上为增函数,由方程g(x)=0在x∈[-4,4]上恰有3个不相等的实数解,可得
,+∞)上为增函数,由方程g(x)=0在x∈[-4,4]上恰有3个不相等的实数解,可得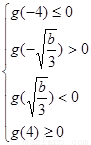 (9分)
(9分)
解得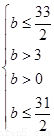 ∴b∈
∴b∈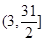 ( 10分 )
( 10分 )
(II)法一:由不等式f(x)+2b≥0,得x3-bx+2b≥0,即(x-2)b≤x3,
(ⅰ)若x-2=0即x=2时,b∈R; (11分)
(ⅱ)若x-2<0即x∈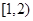 时,b≥
时,b≥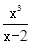 在区间
在区间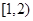 上恒成立,令h(x)=
上恒成立,令h(x)=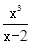 ,则b≥h(x)max。∵h’(x)=
,则b≥h(x)max。∵h’(x)= ,∴h’(x)<0在x∈
,∴h’(x)<0在x∈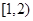 上恒成立,所以h(x)在区间
上恒成立,所以h(x)在区间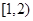 上是减函数,∴h(x)max=h(1)=-1,∴b≥-1。 (13分)
上是减函数,∴h(x)max=h(1)=-1,∴b≥-1。 (13分)
(ⅲ)若x-2>0即x∈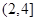 时,b≤
时,b≤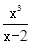 在区间
在区间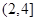 上恒成立,则b≤h(x)min。
上恒成立,则b≤h(x)min。
由(ⅱ)可知,函数h(x)在区间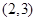 上是减函数,在区间
上是减函数,在区间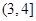 上是增函数,
上是增函数,
∴h(x)min=h(3)=27,∴b≤27 (15分)
综上所述,b∈[-1,27] (16分)
法二: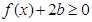
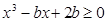 设
设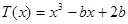
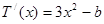 (11分)
(11分)
当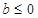 时,
时,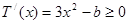 ,
,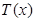 在[1,4]上为增函数,
在[1,4]上为增函数, 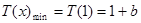 , 所以
, 所以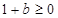 ,
, 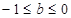 (12分)
(12分)
当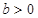 时,
时,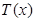 在区间(-∞,-
在区间(-∞,-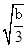 )上为增函数,在区间(-
)上为增函数,在区间(-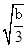 ,
,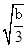 )上为减函数,在区间(
)上为减函数,在区间(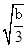 ,+∞)上为增函数,
,+∞)上为增函数,
若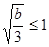 ,即
,即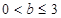 时,
时,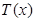 在[1,4]上为增函数,
在[1,4]上为增函数, 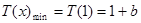
所以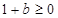 ,
,
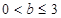 (13分)
(13分)
若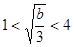 时,
时,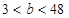 时,
时,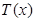 在
在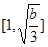 上为减函数,在
上为减函数,在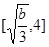 上为增函数,
上为增函数,
所以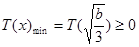 , 得
, 得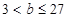 (14分)
(14分)
若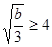 时,即
时,即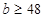 时,
时,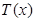 在[1,4]上为减函数,
在[1,4]上为减函数, 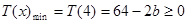 ,
,
得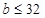 ,舍去。 (15分)
,舍去。 (15分)
故 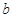 的取值范围是
的取值范围是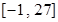 (16分)
(16分)
【解析】略

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.