题目内容
【题目】已知实数![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值是2,则
上的最大值是2,则![]() ______
______
【答案】![]() 或
或![]()
【解析】
由题意可得f(0)≤2,求得a的范围,去掉一个绝对值,再由最值的取得在顶点和端点处,计算得a的值,再检验可得a的值.
因为函数f(x)=|x2+|x﹣a|﹣3|在区间[﹣1,1]上的最大值是2,可得f(0)≤2,
且a>0,得|a﹣3|≤2,解得1≤a≤5,即有f(x)=|x2﹣x+a﹣3|,﹣1≤x≤1,
由f(x)的最大值在顶点或端点处取得,
当f(﹣1)=2,即|a﹣1|=2,解得a=3或﹣1(舍去);
当f(1)=2,即|a﹣3|=2,解得a=5或a=1;
当f(![]() )=2,即|a﹣
)=2,即|a﹣![]() |=2,解得a=
|=2,解得a=![]() 或
或![]() (舍去).
(舍去).
当a=1时,f(x)=|x2﹣x﹣2|,因为f(![]() )=
)=![]() >2,不符题意;(舍去).
>2,不符题意;(舍去).
当a=5时,f(x)=|x2﹣x+2|,因为f(-1)=4>2,不符题意;(舍去).
当a=3时,f(x)=|x2﹣x|,显然当x=﹣1时,取得最大值2,符合题意;
当a=![]() 时,f(x)=|x2﹣x﹣
时,f(x)=|x2﹣x﹣![]() |,f(1)=
|,f(1)=![]() ,f(﹣1)=
,f(﹣1)=![]() ,f(
,f(![]() )=2,符合题意.
)=2,符合题意.
故答案为:3或![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】某小区为了调查居民的生活水平,随机从小区住户中抽取![]() 个家庭,得到数据如下:
个家庭,得到数据如下:
家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
参考公式:回归直线的方程是:![]() ,其中,
,其中,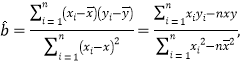
![]() .
.
(1)据题中数据,求月支出![]() (千元)关于月收入
(千元)关于月收入![]() (千元)的线性回归方程(保留一位小数);
(千元)的线性回归方程(保留一位小数);
(2)从这![]() 个家庭中随机抽取
个家庭中随机抽取![]() 个,求月支出都少于
个,求月支出都少于![]() 万元的概率.
万元的概率.

