题目内容
已知数列{an}的通项公式an=3n-50,则其前n项和Sn的最小值是
- A.-784
- B.-392
- C.-389
- D.-368
B
分析:先令3n-50≥0求得数列从地17项开始为正数,前16项为负,推断出数列的前n项的和中,前16项的和最小,进而利用等差数列的求和公式求得答案.
解答:令3n-50≥0求得n>16
即数列从地17项开始为正数,前16项为负,
故数列的前16项的和最小,
a16=-2,a1=-47
∴S16=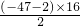 =-392
=-392
故选B
点评:本题主要考查了等差数列的性质,求和公式以及数列与不等式的综合.解题的关键是分析出数列的正数项或负数项.
分析:先令3n-50≥0求得数列从地17项开始为正数,前16项为负,推断出数列的前n项的和中,前16项的和最小,进而利用等差数列的求和公式求得答案.
解答:令3n-50≥0求得n>16
即数列从地17项开始为正数,前16项为负,
故数列的前16项的和最小,
a16=-2,a1=-47
∴S16=
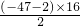 =-392
=-392故选B
点评:本题主要考查了等差数列的性质,求和公式以及数列与不等式的综合.解题的关键是分析出数列的正数项或负数项.

练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|