Question

7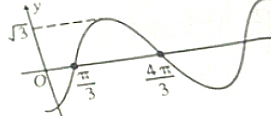．设函数f（x）=Asin（ωx+φ）x∈R，ω＞0，|φ|＜π），其导函数y=f′（x）的部分图象如图所示，
（1）求f（x）的解析式；
（2）求函数g（x）=e^x•f（x）的单调递减区间．

Answer 1

分析 （1）根据函数f（x）的导函数f′（x）的图象，求出周期T与ω、A的值，再利用点的坐标求出φ的值即可；
（2）求出g（x）的导数g′（x），利用g′（x）≤0求出g（x）的单调递减区间．

解答 解：（1）f（x）=Asin（ωx+φ）的导函数f′（x）=Aωcos（ωx+φ），
由图象知T=2（$\frac{4π}{3}$-$\frac{π}{3}$）=2π，
所以2π=$\frac{2π}{ω}$，得ω=1，
又Aω=$\sqrt{3}$，A=$\sqrt{3}$，
又（$\frac{\frac{π}{3}+\frac{4π}{3}}{2}$，$\sqrt{3}$）在图象上，
所以$\sqrt{3}$=$\sqrt{3}$cos（$\frac{5π}{6}$+φ），
即φ=-$\frac{5π}{6}$+2kπ，k∈Z；
所以取φ=-$\frac{5π}{6}$，
所以f（x）=$\sqrt{3}$sin（x-$\frac{5π}{6}$）；
（2）∵函数g（x）=e^x•f（x）=e^x•$\sqrt{3}$sin（x-$\frac{5π}{6}$），
∴g′（x）=$\sqrt{3}$e^x（sin（x-$\frac{5π}{6}$）+cos（x-$\frac{5π}{6}$））；
令g′（x）≤0，得sin（x-$\frac{5π}{6}$）+cos（x-$\frac{5π}{6}$）≤0，
即$\sqrt{2}$sin（x-$\frac{5π}{6}$+$\frac{π}{4}$）≤0，
∴sin（x-$\frac{7π}{12}$）≤0，
解得-π+2kπ≤x-$\frac{7π}{12}$≤2kπ，k∈Z，
即-$\frac{5π}{12}$+2kπ≤x≤$\frac{7π}{12}$+2kπ，k∈Z；
∴g（x）的单调递减区间是[-$\frac{5π}{12}$+2kπ，$\frac{7π}{12}$+2kπ]，k∈Z．

点评 本题考查了三角函数的图象与性质的应用问题，也考查了利用导数求函数的单调区间的应用问题，是中档题目．