题目内容
【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：
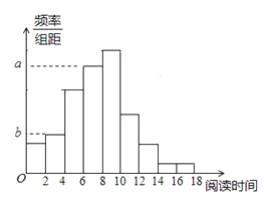
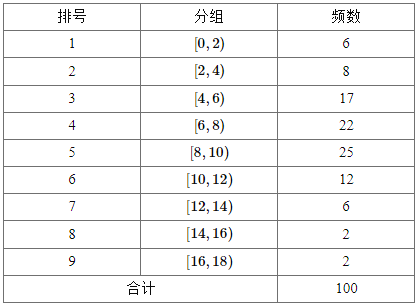
（1）求频率分布直方图中的
，
的值；
（2）从阅读时间在
的学生中任选2人，求恰好有1人阅读时间在
，另1人阅读时间在
的概率.
【答案】(1)a=0.11,b=0.04;(2)
.
【解析】
课外阅读时间落在
，
的有22人，频率为0.22，由此能求出
，课外阅读时间落在
，
的有8人，频率为0.08，由此能求出
；
课外阅读时间落在
，
的有2人，设为
，
；课外阅读时间落在
，
的有2人为
，
，由此利用列举法能求出从课外阅读时间落在，的学生中任选2人，其中恰好有1人阅读时间在，，另1人阅读时间在，的概率．
课外阅读时间落在，的有22人，频率为0.22，
所以
课外阅读时间落在，的有8人，频率为0.08，
所以
课外阅读时间落在，的有2人，设为，；课外阅读时间落在，的有2
人为，，
则从课外阅读时间落在，的学生中任选2人包含：
，
，
，
，
，
共6种，
其中恰好有1人阅读时间在，，
另1人阅读时间在，的有，，，共4种，
所以所求概率为：
．
练习册系列答案
相关题目
