题目内容
【题目】在四面体S﹣ABC中,SA⊥平面ABC,∠BAC=120°,SA=AC=2,AB=1,则该四面体的外接球的表面积为
A. 11π B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵AC=2,AB=1,∠BAC=120°,
∴BC=![]() ,
,
∴三角形ABC的外接圆半径为r,2r=![]() ,r=
,r=![]() ,
,
∵SA⊥平面ABC,SA=2,
由于三角形OSA为等腰三角形,O是外接球的球心.
则有该三棱锥的外接球的半径R=![]() ,
,
∴该三棱锥的外接球的表面积为S=4πR2=![]() .
.
选D.
点睛:空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(2)若球面上四点![]() 构成的三条线段
构成的三条线段![]() 两两互相垂直,且
两两互相垂直,且![]() ,一般把有关元素“补形”成为一个球内接长方体,利用
,一般把有关元素“补形”成为一个球内接长方体,利用![]() 求解.
求解.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某学校的特长班有![]() 名学生,其中有体育生
名学生,其中有体育生![]() 名,艺术生
名,艺术生![]() 名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于
名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于![]() 次/分到
次/分到![]() 次/分之间.现将数据分成五组,第一组
次/分之间.现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五章
,…,第五章![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
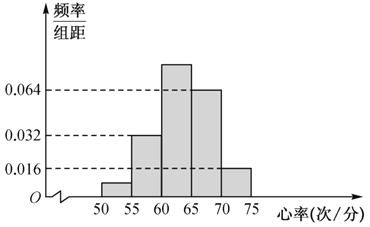
(1)求![]() 的值,并求这
的值,并求这![]() 名同学心率的平均值;
名同学心率的平均值;
(2)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为![]() ,请将下面的列联表补充完整,并判断是否有
,请将下面的列联表补充完整,并判断是否有![]() 的把握认为心率小于
的把握认为心率小于![]() 次/分与常年进行系统的身体锻炼有关?说明你的理由.
次/分与常年进行系统的身体锻炼有关?说明你的理由.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.



