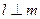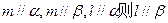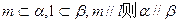题目内容
(本小题满分14分)
如右图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,∠PDA=30°,点F是PB的中点,
点E在边BC上,
(Ⅰ)若E为BC中点,证明:EF∥平面PAC;
(Ⅱ)证明:AF⊥平面PBC;
(Ⅲ)当BE等于何值时,二面角P—DE—A的大小为45°?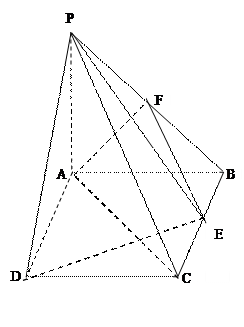
如右图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,∠PDA=30°,点F是PB的中点,
点E在边BC上,
(Ⅰ)若E为BC中点,证明:EF∥平面PAC;
(Ⅱ)证明:AF⊥平面PBC;
(Ⅲ)当BE等于何值时,二面角P—DE—A的大小为45°?

(Ⅰ)略
(Ⅱ)略
(Ⅲ)当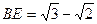 时,二面角P-DE-A的大小为45°。
时,二面角P-DE-A的大小为45°。
(Ⅱ)略
(Ⅲ)当
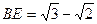 时,二面角P-DE-A的大小为45°。
时,二面角P-DE-A的大小为45°。解法一:
(Ⅰ)解:
∵在△PBC中,E、F分别为BC、PB的中点 ∴EF∥PC
又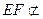 平面PAC,
平面PAC,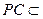 平面PAC ∴EF∥平面PAC
平面PAC ∴EF∥平面PAC
(Ⅱ)证明:∵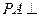 平面
平面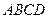 ,
,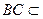 平面
平面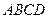 ∴
∴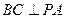 ………(4分) ∵
………(4分) ∵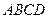 是矩形 ∴
是矩形 ∴
又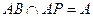 ,∴
,∴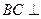 平面PAB, ……(5分)
平面PAB, ……(5分)
又AF 平面PAB∴BC⊥AF 又PA=AB=1,且点F是PB的中点 ∴PB⊥AF ……(7分)
平面PAB∴BC⊥AF 又PA=AB=1,且点F是PB的中点 ∴PB⊥AF ……(7分)
又∵PB∩BC=B,PB、BC 平面PBE
平面PBE
∴AF⊥平面PBC
(Ⅲ)解:当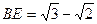 时,二面角P-DE-A的大小为45° 过A作AG⊥DE于G,连结PG
时,二面角P-DE-A的大小为45° 过A作AG⊥DE于G,连结PG
又∵DE⊥PA ∴DE⊥平面PAG ∴DE⊥PG
则∠PGA是二面角P-DE-A的平面角 ∴∠PGA=45° ∵∠PDA=30°
,PA=AB=1,∴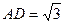 ∴
∴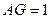 ,
,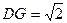 设BE=
设BE=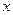 ,则GE=
,则GE=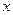 ,CE=
,CE=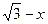 ,在
,在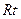 △DCE中,
△DCE中,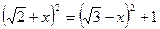
解得: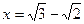 或
或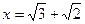 (舍去)
(舍去)
故当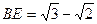 时,二面角P-DE-A的大小为45°解法二:(Ⅰ)与解法一同
时,二面角P-DE-A的大小为45°解法二:(Ⅰ)与解法一同
(Ⅱ)证明:以A为坐标原点,分别以AD、AB、AP所在直线为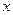 轴、
轴、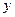 轴、
轴、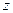 轴
轴
建立空间直角坐标系,则P(0,0,1),B(0,1,0),F(0,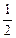 ,
,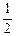 ),
),
D(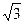 ,0,0) 设
,0,0) 设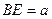 ,则E(
,则E(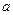 ,1,0)
,1,0)
∴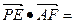 (
(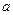 ,1,-1)
,1,-1)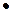 (0,
(0,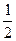 ,
,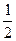 )=
)=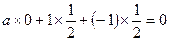
∴AF⊥PE (Ⅲ)解:设平面PDE的一个法向量为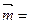 (
(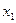 ,
,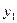 ,
,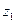 ),
),
则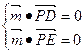 又
又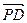 =(
=(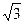 ,0,-1)
,0,-1)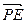 =(
=(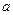 ,1,-1)
,1,-1)
∴
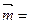 (1,
(1,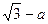 ,
,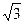 )
)
而平面ADE的一个法向量为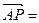 (0,0,1)又二面角P-DE-A的大小为45°
(0,0,1)又二面角P-DE-A的大小为45°
∴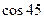 °=
°=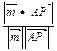 即
即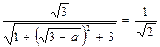 ∴
∴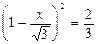 即
即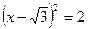 解得
解得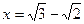 或
或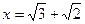 (舍去)
(舍去)
故当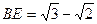 时,二面角P-DE-A的大小为45°。
时,二面角P-DE-A的大小为45°。
(Ⅰ)解:
|
|
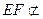 平面PAC,
平面PAC,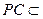 平面PAC ∴EF∥平面PAC
平面PAC ∴EF∥平面PAC
|
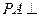 平面
平面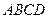 ,
,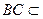 平面
平面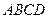 ∴
∴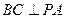 ………(4分) ∵
………(4分) ∵ 是矩形 ∴
是矩形 ∴
又
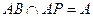 ,∴
,∴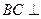 平面PAB, ……(5分)
平面PAB, ……(5分)
|
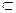 平面PAB∴BC⊥AF 又PA=AB=1,且点F是PB的中点 ∴PB⊥AF ……(7分)
平面PAB∴BC⊥AF 又PA=AB=1,且点F是PB的中点 ∴PB⊥AF ……(7分) 又∵PB∩BC=B,PB、BC
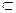 平面PBE
平面PBE
|
|
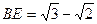 时,二面角P-DE-A的大小为45° 过A作AG⊥DE于G,连结PG
时,二面角P-DE-A的大小为45° 过A作AG⊥DE于G,连结PG 又∵DE⊥PA ∴DE⊥平面PAG ∴DE⊥PG
|
|
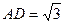 ∴
∴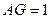 ,
,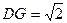 设BE=
设BE=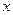 ,则GE=
,则GE=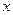 ,CE=
,CE=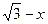 ,在
,在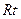 △DCE中,
△DCE中,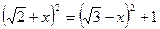
|
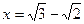 或
或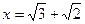 (舍去)
(舍去)
|
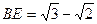 时,二面角P-DE-A的大小为45°解法二:(Ⅰ)与解法一同
时,二面角P-DE-A的大小为45°解法二:(Ⅰ)与解法一同(Ⅱ)证明:以A为坐标原点,分别以AD、AB、AP所在直线为
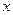 轴、
轴、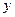 轴、
轴、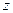 轴
轴建立空间直角坐标系,则P(0,0,1),B(0,1,0),F(0,
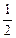 ,
,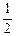 ),
),
|
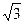 ,0,0) 设
,0,0) 设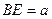 ,则E(
,则E(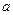 ,1,0)
,1,0)∴
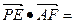 (
(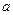 ,1,-1)
,1,-1)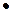 (0,
(0,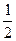 ,
,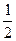 )=
)=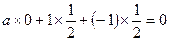
|
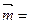 (
(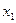 ,
,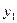 ,
,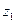 ),
),则
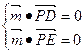 又
又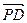 =(
=(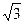 ,0,-1)
,0,-1)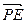 =(
=(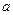 ,1,-1)
,1,-1)
|

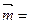 (1,
(1,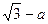 ,
,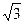 )
)
|
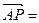 (0,0,1)又二面角P-DE-A的大小为45°
(0,0,1)又二面角P-DE-A的大小为45°
|
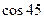 °=
°=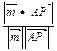 即
即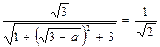 ∴
∴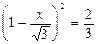 即
即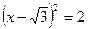 解得
解得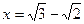 或
或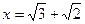 (舍去)
(舍去)
|
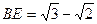 时,二面角P-DE-A的大小为45°。
时,二面角P-DE-A的大小为45°。
练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目

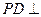 平面
平面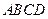 ,
,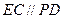 ,且
,且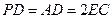 ="2" .
="2" .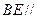 平面
平面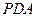 .
. 
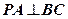 ;
;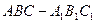 的侧棱长和底面边长均为2, N为侧棱
的侧棱长和底面边长均为2, N为侧棱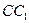 上的点,若平面
上的点,若平面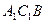 与平面
与平面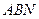 所成二面角(锐角)的余弦值为
所成二面角(锐角)的余弦值为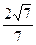 ,试确定点N的位置。
,试确定点N的位置。
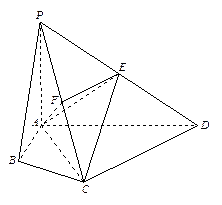
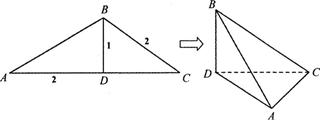
 中,
中,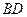 为AC边上的高,
为AC边上的高,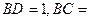
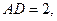 沿BD将
沿BD将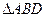 翻折,使得
翻折,使得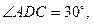 得到几何体
得到几何体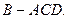
 ,E、F分别为正方体的面
,E、F分别为正方体的面 、面
、面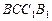 的中心,则四边形
的中心,则四边形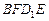 在该正方体的面上的射影可能是
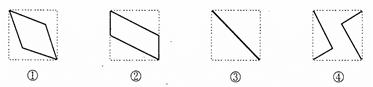
在该正方体的面上的射影可能是 __________ (只写出序号即可)
__________ (只写出序号即可)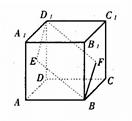
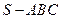 ,若空间一点
,若空间一点 满足
满足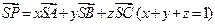 ,则
,则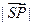 的最小值为
的最小值为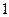

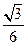
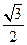
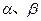 是两个不重合的平面,
是两个不重合的平面,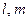 为不重合的直线,则下列命题正确的( )
为不重合的直线,则下列命题正确的( ) 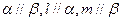 ,则
,则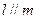
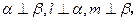 ,则
,则