题目内容
甲、乙两人各射击一次,击中目标的概率分别是 .假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
.假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
 .假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
.假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.(1)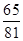 (2)
(2) 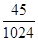 (3)
(3)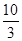
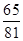 (2)
(2) 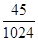 (3)
(3)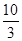
【错解分析】概率题常常有如下几种类型:①等可能性事件的概率;②互斥事件的概率;③独立事件同时发生的概率;④独立重复试验事件的概率.弄清每种类型事件的特点,区分使用概率求法,如本题的第一问是一个独立事件同时发生的问题,满足几何显著条件:每次射中目标都是相互独立的、可以重复射击即事件重复发生、每次都只有发生或不发生两种情形且发生的概率是相同的.第二问解答时要认清限制条件的意义.
【正解】本小题主要考查概率的计算、离散型随机变量的分布列、数学期望的概念及其计算,考查分析问题及解决实际问题的能力,读题、想题、审题的能力,求随机变量的概率在某种程度上就是正确求出相应事件的概率,因此必须弄清每个取值的含义,本概率题跟排列组合知识联系紧密,其实高中概率题往往以排列组合知识为前提.
(1)记“甲连续射击4次,至少1次未击中目标”为事件A1,由题意,射击4次,相当于4次独立重复试验,故P(A1)=
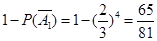
答:甲射击4次,至少1次未击中目标的概率为
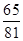 ;
;(2) 记“乙恰好射击5次后,被中止射击”为事件A3,“乙第i次射击未击中” 为事件Di,(i=1,2,3,4,5),则
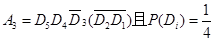 ,由于各事件相互独立,
,由于各事件相互独立,故
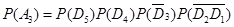
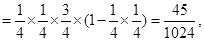
答:乙恰好射击5次后,被中止射击的概率是
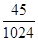
(3)根据题意ξ服从二项分布;Eξ=5×
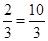

练习册系列答案
相关题目
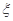 ~
~ ,统计结果显示
,统计结果显示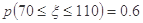 ,则
,则 ( )
( )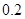
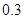
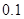
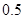
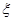 的分布列,并求李明在一年内领到驾照的概率.
的分布列,并求李明在一年内领到驾照的概率.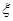 服从正态分布
服从正态分布 .若
.若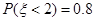 ,则
,则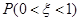 的值为( )
的值为( ) 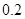
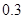
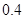
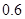
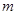 ,第二次出现的点数记为
,第二次出现的点数记为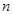 ,方程组
,方程组 只有一组解的概率是_________.(用最简分数表示)
只有一组解的概率是_________.(用最简分数表示) 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满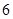 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为 .
. 的值;
的值; 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量 。
。