题目内容
【题目】有限个元素组成的集合为![]() ,
,![]() ,集合
,集合![]() 中的元素个数记为
中的元素个数记为![]() ,定义
,定义![]() ,集合
,集合![]() 的个数记为
的个数记为![]() ,当
,当![]() ,称集合
,称集合![]() 具有性质
具有性质![]() .
.
(1)设集合![]() 具有性质
具有性质![]() ,判断集合
,判断集合![]() 中的三个元素是否能组成等差数列,请说明理由;
中的三个元素是否能组成等差数列,请说明理由;
(2) 设正数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,其中
,其中![]() ,数列
,数列![]() 中的前
中的前![]() 项:
项:![]() 组成的集合
组成的集合![]() 记作
记作![]() ,将集合
,将集合![]() 中的所有元素
中的所有元素![]() 从小到大排序,即
从小到大排序,即![]() 满足
满足![]() ,求
,求![]() ;
;
(3) 己知集合![]() ,其中数列
,其中数列![]() 是等比数列,
是等比数列,![]() ,且公比是有理数,判断集合
,且公比是有理数,判断集合![]() 是否具有性质
是否具有性质![]() ,说明理由.
,说明理由.
【答案】(1)否,见解析;(2)![]() ;(3)具有性质
;(3)具有性质![]() ,理由见解析
,理由见解析
【解析】
(1)根据集合![]() 具有性质
具有性质![]() ,可以得到
,可以得到![]() 、以及
、以及![]() 的元素性质,运用反证法可以判断出集合
的元素性质,运用反证法可以判断出集合![]() 中的三个元素不能组成等差数列;
中的三个元素不能组成等差数列;
(2)根据递推公式求出数列![]() 的通项公式,根据题意写出集合
的通项公式,根据题意写出集合![]() ,根据题目中所给的定义,结合等比数列的性质求出
,根据题目中所给的定义,结合等比数列的性质求出![]() ;
;
(3)只要能够证明当![]() 时,
时,![]() 不成立,运用反证法结合整除的知识,就可以判断出集合
不成立,运用反证法结合整除的知识,就可以判断出集合![]() 具有性质
具有性质![]() .
.
(1)集合![]() 中的三个元素不能组成等差数列,理由如下:
中的三个元素不能组成等差数列,理由如下:
因为集合![]() 具有性质
具有性质![]() ,所以
,所以![]() ,由题中所给的定义可知:
,由题中所给的定义可知:![]() 中的元素应是:
中的元素应是:![]() 这6个元素应该互不相等,假设
这6个元素应该互不相等,假设![]() 中的三个元素能构成等差数列,不妨设
中的三个元素能构成等差数列,不妨设![]() 成等差数列,这时有
成等差数列,这时有
![]() 这与集合元素集合中的6个元素互不相等矛盾,其它二种情况也是一样,故
这与集合元素集合中的6个元素互不相等矛盾,其它二种情况也是一样,故![]() 中的三个元素不能能构成等差数列;
中的三个元素不能能构成等差数列;
(2)![]() ,
,![]() 得:
得:
![]() ,说明数列从第二项起,数列
,说明数列从第二项起,数列![]() 是等差数列,
是等差数列,
因为![]() ,
,![]() ,所以有
,所以有![]() ,所以
,所以![]() ,显然
,显然![]() 也成立,因此
也成立,因此![]() .
.
所以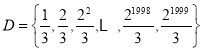
![]() ,显然
,显然![]()
根据定义在![]() 之间增加的元素个数为:
之间增加的元素个数为:![]() ,这样包括
,这样包括![]() 在内前面一共有
在内前面一共有![]() 个元素.
个元素.
当![]() 时,包括
时,包括![]() 在内前面共有2016个,显然不到第2020个数,所以只有当
在内前面共有2016个,显然不到第2020个数,所以只有当![]() 时,能找到
时,能找到
因此![]() ;
;
(3)集合![]() 具有性质
具有性质![]() ,理由如下:设等比数列
,理由如下:设等比数列![]() 的公比为
的公比为![]() ,所以通项公式为:
,所以通项公式为:![]() ,
,![]() 为有理数.
为有理数.
设假设当![]() 时,
时,![]() 成立,则有
成立,则有
![]() ,
,![]()
因为![]() 为有理数,所以设
为有理数,所以设![]()
![]() 且
且![]() 互质,因此有
互质,因此有
![]() ,
,
式子的左边是![]() 的倍数,右边是
的倍数,右边是![]() 的倍数,而
的倍数,而![]() 互质,显然
互质,显然![]() 不成立,因此
不成立,因此![]() 集合中的元素个数为:
集合中的元素个数为:![]() ,因此它符合已知所下的定义,因此集合
,因此它符合已知所下的定义,因此集合![]() 是否具有性质
是否具有性质![]() .
.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案