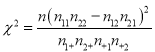题目内容
【题目】某学生参加某高校的自主招生考试，须依次参加A、B、C、D、E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A、B、C、D四项考试不合格的概率均为
，参加第五项不合格的概率为
（1）求该生被录取的概率；
（2）记该生参加考试的项数为
，求的分布列和期望．
【答案】（1）
（2）
【解析】
（1）若该生被录取，则前四项最多有一项不合格，并且第五项必须合格
记A={前四项均合格}，B={前四项中仅有一项不合格}
则
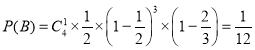
又A、B互斥，故所求概率为
，
所以该生被录取的概率是；
（2）该生参加考试的项数
可以是2，3，4，5.
，
，
| 2 | 3 | 4 | 5 |
|
|
|
|
|
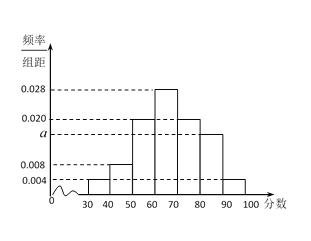
直通贵州名校周测月考直通名校系列答案
【题目】改革开放40年，我国经济取得飞速发展，城市汽车保有量在不断增加，人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识，某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各50人，进行问卷测评，所得分数的频率分布直方图如图所示.规定得分在80分以上为交通安全意识强.
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
（Ⅰ）求
的值，并估计该城市驾驶员交通安全意识强的概率；
（Ⅱ）已知交通安全意识强的样本中男女比例为4:1，完成2×2列联表，并判断有多大把握认为交通安全意识与性别有关；
（Ⅲ）在（Ⅱ）的条件下，从交通安全意识强的驾驶员中随机抽取2人，求抽到的女性人数
的分布列及期望.
附：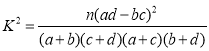
，其中
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查，下表是在某单位调查后得到的数据(人数)：
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
（1）能否有90%以上的把握认为对这一问题的看法与性别有关?
（2）进一步调查：
①从赞同“男女延迟退休”的
人中选出
人进行陈述发言，求事件“男士和女士各至少有
人发言”的概率；
②从反对“男女延迟退休”的
人中选出人进行座谈，设选出的人中女士人数为
，求的分布列和数学期望.
附：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
