题目内容
已知动点P（x、y）满足10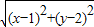
=|3x+4y+2|，则动点P的轨迹是（ ）A．椭圆
B．双曲线
C．抛物线
D．无法确定
【答案】分析：将动点M的方程进行等价转化，即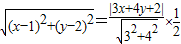 
，等式左边为点M到定点的距离，等式右边为点M到定直线的距离的
，由椭圆定义即可判断M点的轨迹曲线为椭圆．
解答：解：∵10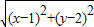
=|3x+4y+2|，，即 
，
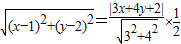其几何意义为点M（x，y）到定点（1，2）的距离等于到定直线3x+4y+2=0的距离的
，
由椭圆的定义，点M的轨迹为以（1，2）为焦点，以直线3x+4y+2=0为准线的椭圆，
故选A．
点评：本题考察了椭圆的定义，解题时要能从形式上辨别两点间的距离公式和点到直线的距离公式．
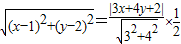，等式左边为点M到定点的距离，等式右边为点M到定直线的距离的，由椭圆定义即可判断M点的轨迹曲线为椭圆．解答：解：∵10
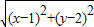=|3x+4y+2|，，即 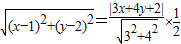，其几何意义为点M（x，y）到定点（1，2）的距离等于到定直线3x+4y+2=0的距离的
，由椭圆的定义，点M的轨迹为以（1，2）为焦点，以直线3x+4y+2=0为准线的椭圆，
故选A．
点评：本题考察了椭圆的定义，解题时要能从形式上辨别两点间的距离公式和点到直线的距离公式．
练习册系列答案
相关题目