Question

已知动点P（x，y）在椭圆C：

x2

25

+

y2

16

=1上，F为椭圆C的右焦点，若点M满足|

MF

|=1且

MP

•

MF

=0，则|

PM

|的最小值为（　　）

• A、

  3

• B、3
• C、

  12

  5

• D、1

Answer 1

分析：依题意知，该椭圆的焦点F（3，0），点M在以F（3，0）为圆心，1为半径的圆上，当PF最小时，切线长PM最小，作出图形，即可得到答案．

解答：解：依题意知，点M在以F（3，0）为圆心，1为半径的圆上，PM为圆的切线，
∴当PF最小时，切线长PM最小．

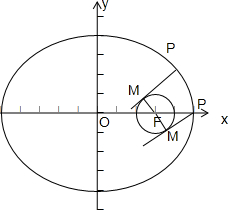
由图知，当点P为右顶点（5，0）时，|PF|最小，最小值为：5-3=2．
此时|PM|=

22-12

=

3

．
故选：A．

点评：本题考查椭圆的标准方程、圆的方程，考查作图与分析问题解决问题的能力，属于中档题．