题目内容
已知动点P(x,y)满足,
+
=
,则
取值范围( )
| x2+y2-4x+6y+13 |
| x2+y2+6x+4y+13 |
| 26 |
| y-1 |
| x-3 |
分析:由于动点P(x,y)满足,
+
=
,化为
+
=
.设A(2,-3),B(-3,-2),可得|AB|=
=
.可知动点P(x,y)在相等AB上,设k=
,则k表示动点P(x,y)与M(3,1)连线的斜率.因此kMB≤k≤kMA,利用斜率计算公式即可得出.
| x2+y2-4x+6y+13 |
| x2+y2+6x+4y+13 |
| 26 |
| (x-2)2+(y+3)2 |
| (x+3)2+(y+2)2 |
| 26 |
| (-3-2)2+(-2+3)2 |
| 26 |
| y-1 |
| x-3 |
解答:解:由于动点P(x,y)满足,
+
=
,化为
+
=
,
设A(2,-3),B(-3,-2),则|AB|=
=
.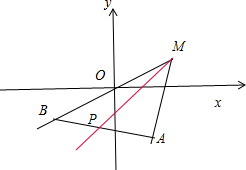
∴动点P(x,y)在相等AB上,
设k=
,则k表示动点P(x,y)与M(3,1)连线的斜率.
又kMA=
=4,kMB=
=
.
∴
≤k≤4.
∴
∈[
,4].
故选C.
| x2+y2-4x+6y+13 |
| x2+y2+6x+4y+13 |
| 26 |
| (x-2)2+(y+3)2 |
| (x+3)2+(y+2)2 |
| 26 |
设A(2,-3),B(-3,-2),则|AB|=
| (-3-2)2+(-2+3)2 |
| 26 |

∴动点P(x,y)在相等AB上,
设k=
| y-1 |
| x-3 |
又kMA=
| -3-1 |
| 2-3 |
| -2-1 |
| -3-3 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
| y-1 |
| x-3 |
| 1 |
| 2 |
故选C.
点评:本题考查了两点间的距离公式、直线的斜率计算公式等基础知识与基本技能方法,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目