题目内容
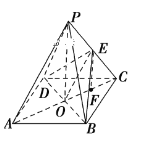
【题目】如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面边长为a，E是PC的中点．
(1)求证：PA∥平面BDE；
(2)求证：平面PAC⊥平面BDE．
【答案】（1）证明见解析；（2）证明见解析．
【解析】
(1) 连结OE，证明OE∥PA，即证PA∥平面BDE.(2)先证明BD⊥平面PAC，再证明平面PAC⊥平面BDE．
(1)证明：连结OE，如图所示．
∵O，E分别为AC，PC的中点，
∴OE∥PA.
∵OE平面BDE，PA平面BDE，
∴PA∥平面BDE.
(2)证明：∵PO⊥平面ABCD，
∴PO⊥BD.
在正方形ABCD中，BD⊥AC.
又∵PO∩AC＝O，
∴BD⊥平面PAC.
又∵BD平面BDE，
∴平面PAC⊥平面BDE.
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】为利于分层教学，某学校根据学生的情况分成了A，B,C三类，经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成缎，其统计表如下：
A类
第x次 | 1 | 2 | 3 | 4 | 4 |
分数y（满足150） | 145 | 83 | 95 | 72 | 110 |
，
；
B类
第x次 | 1 | 2 | 3 | 4 | 4 |
分数y（满足150） | 85 | 93 | 90 | 76 | 101 |
，
；
C类
第x次 | 1 | 2 | 3 | 4 | 4 |
分数y（满足150） | 85 | 92 | 101 | 100 | 112 |
，
；
（1）经计算己知A，B的相关系数分别为
，
．，请计算出C学生的
的相关系数，并通过数据的分析回答抽到的哪类学生学习成绩最稳定；（结果保留两位有效数字，
越大认为成绩越稳定）
（2）利用（1）中成绩最稳定的学生的样本数据，已知线性回归直线方程为
，利用线性回归直线方程预测该生第十次的成绩．
附相关系数
，线性回归直线方程
，
，
．
