题目内容
【题目】对于四面体
，有以下命题：①若AB=AC=AD，则AB，AC，AD与底面所成的角相等；②若AB⊥CD，AC⊥BD，则点A在底面BCD内的射影是△BCD的内心；③四面体的四个面中最多有四个直角三角形；④若四面体的6条棱长都为1，则它的内切球的表面积为
，其中正确的命题是
A. ①③ B. ③④ C. ①②③ D. ①③④
【答案】D
【解析】①正确，若AB=AC=AD，则AB，AC，AD在底面的射影相等，即与底面所成角相等；
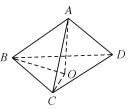
②不正确，如图，点A在平面BCD的射影为点O，连接BO，CO，可得BO⊥CD，CO⊥BD，所以点O是△BCD的垂心；
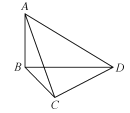
③正确，如图，若AB⊥平面BCD，∠BCD=90°，则四面体
的四个面均为直角三角形；
④正确，正四面体的内切球的半径为r，棱长为1，高为
，根据等体积公式
，解得
，那么内切球的表面积
. 故正确的命题是①③④.故选D.
练习册系列答案
相关题目
