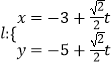题目内容
【题目】某地区工会利用“健步行
” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分)， 每多走2千步再积20分（不足2千步不积分).为了解会员的健步走情况，工会在某天从系统中随机抽取了 1000名会员，统计了当天他们的步数，并将样本数据分为
，
九组，整理得到如图频率分布直方图：
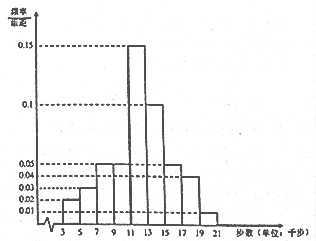
（1）求当天这1000名会员中步数少于11千步的人数；
（2）从当天步数在
的会员中按分层抽样的方式抽取6人，再从这6人中随机抽取2人，求这2人积分之和不少于200分的概率；
（3）写出该组数据的中位数（只写结果）.
【答案】（1）300（2）
（3）
【解析】分析：(1)根据直方图的性质，求出每个小矩形的面积可得到健步走的步数在
内的频率，
健步走的步数在
内的频率，健步走的步数在
内的频率，健步走的步数在
内的频率，从而可得结果；（2）按分层抽样的方法，在
内应抽取3人，在
内应抽取2人，在
内应抽取1人，利用列举法
人中任意选取
人共有
种，其中这2人的积分之和不少于
的情况共有
种，由古典概型概率公式可得结果；（3）根据频率分布直方图的性质能求出中位数.
详解：（Ⅰ）这1000名会员中健步走的步数在内的人数为
；
健步走的步数在内的人数为
；
健步走的步数在内的人数为
；
健步走的步数在内的人数为；
．
所以这1000名会员中健步走的步数少于11千步的人数为300人．
（Ⅱ）按分层抽样的方法，在内应抽取3人，记为
，
，
，每人的积分是90分；在内应抽取2人，记为
，
，每人的积分是110分；
在内应抽取1人，记为
，每人的积分是130分；
从6人中随机抽取2人，有
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共15种方法．
所以从6人中随机抽取2人，这2人的积分之和不少于200分的有，，，
，，，，，，，，共12种方法．
设从6人中随机抽取2人，这2人的积分之和不少于200分为事件
，则
．
所以从6人中随机抽取2人，这2人的积分之和不少于200分的概率为．
（Ⅲ）中位数为．
应用题作业本系列答案
