��Ŀ����
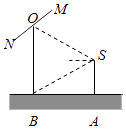
����Ŀ����ͼ��ԲO��һ�뾶Ϊ10��Բ�β�ƺ��Ϊ�������ܱ��������㳡�����Ҫ���ֹ滮�ڲ�ƺ�Ͻ�һ���㳡���㳡��״��ͼ�����߲�����ʾ�������ı��Σ�����A��B�����ڡ�O�ϣ�A��B��C��Dǡ��һ�������ε��ĸ����㣮���ݹ滮Ҫ����A��B��C��D�ĵ㴦��װ��յ�����豸����Բ��O��������ڵ�������4����A��B��C��D�ĵ���·OA��OB��OC��OD��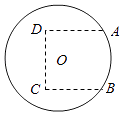
��1���������α߳�Ϊ10�ף���㳡�������
��2���������4����·OA��OB��OC��OD�ܳ��ȵ���Сֵ��
���𰸡�
��1���⣺����AB��
��AB=10����������ABCD�����Ϊ100��
��OA=OB=10�����AOB���������� ![]() ��
��
��Բ�����Ϊ100�У�������AOB�����Ϊ ![]() ��
��
��������AOB�����Ϊ ![]() ��
��
������Ϊ ![]() ��
��
��㳡���Ϊ100+ ![]() ��ƽ���ף���
��ƽ���ף���
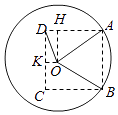
��2����O��OK��CD������ΪK����O��OH��AD�������ӳ��ߣ�������ΪH��
���OAD=�ȣ�0���ȣ� ![]() ����
����
��OH=10sin�ȣ�AH=10cos�ȣ�
��DH=|AD��AH|=|2OH��AH|=|20sin�ȩ�10cos��|��
��OD= ![]() =
= ![]() ��
��
�൱��= ![]() ʱ��
ʱ�� ![]() ��
��
�������4����·OA��OB��OC��OD�ܳ��ȵ���СֵΪ ![]() ���ף���
���ף���
����������1�����㳡�������Ϊ�������빭�ε�����ͣ���������������������ȥ�����ε���������㣻��2�������4����·OA��OB��OC��OD��OA��OBΪԲ�İ뾶����OC��OD������ȣ��������OC��OD����Сֵ�������4����·�ܳ��ȵ���Сֵ .
�����㾫�����������⣬������Ҫ�˽�ֱ����Բ������λ�ù�ϵ(ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е�)��