题目内容
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在[80,90)的人数为12人.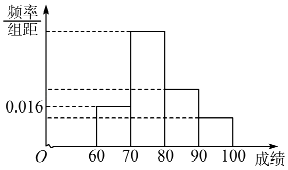
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为X,求X的分布列和数学期望.
【答案】解:(Ⅰ)落在区间[80,90)的频率是 ![]() ,
,
所以人数 ![]() .
.
(Ⅱ)由(Ⅰ)知,参加决赛的选手共6人,
(i)设“甲不在第一位,乙不在最后一位”为事件A,
则 ![]() ,
,
所以甲不在第一位、乙不在最后一位的概率为 ![]() .
.
(ii)随机变量的可能取值为0,1,2, ![]() ,
, ![]() ,
, ![]() ,
,
随机变量X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
因为 ![]() ,
,
所以随机变量的数学期望为1.
【解析】(Ⅰ)由图可知落在区间[80,90)的频率的值即可得出人数。(Ⅱ)由(Ⅰ)可知参加决赛的人有6人(i)根据题意利用相互独立与互斥事件的概率计算出即可得出满足题意的概率。(ii)由已知可得出随机变量的可能取值为0,1,2,利用伯努利概率公式即可计算出各个概率进而可得到随机变量X的分布列,再由数学期望公式即可得到数学期望值。
【考点精析】根据题目的已知条件,利用频率分布直方图和离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案