��Ŀ����
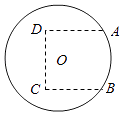
����Ŀ����ͼ��ʾ����Ӱ������S��ij��A����������ǰ��B����һ�����������������O�����Ǻ������ײ�B�ĸ��Ǿ�Ϊ ![]() ����S���۾�������ľ���Ϊ
����S���۾�������ľ���Ϊ ![]() ��
��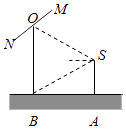
��1������Ӱ�����ߵ�������ˮƽ����������ĸ߶ȣ�
��2�������Ķ�����һ��2�IJʸ�MN�����е�O��S���������ڵ�ƽ������ת����Ӱ��������һ�ӽǷ�ΧΪ ![]() �ľ�ͷ���ڲʸ�ת��������ʱ�̣���Ӱ�������Ƿ��Խ��ʸ�ȫ�����뻭�棿��˵�����ɣ�
�ľ�ͷ���ڲʸ�ת��������ʱ�̣���Ӱ�������Ƿ��Խ��ʸ�ȫ�����뻭�棿��˵�����ɣ�
���𰸡�
��1���⣺��ͼ����SC��ֱOB��C�����CSB= ![]() ����ASB=
����ASB= ![]() ����SA=
����SA= ![]() ��
��
����Rt��SAB�У������BA=3������Ӱ�����ߵ�������ˮƽ����Ϊ3�ף���SC=3����CSO= ![]() ����Rt��SCO�У������OC=
����Rt��SCO�������OC= ![]() ��
��
��ΪBC=SA= ![]() ����OB=2
����OB=2 ![]() ����������Ϊ2
����������Ϊ2 ![]() ��
��
��2���⣺��ͼ������SM��SN����SN=a��SM=b���ɣ�1��֪SO=2 ![]() ��
��
�ڡ�SOM�͡�SON�У�cos��SOM=��cos��SON��
�� ![]() =��
=�� ![]() ���ɵ�a2+b2=26��
���ɵ�a2+b2=26��
�ڡ�MSN�У�cos��MSN= ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
�� ![]() �����ҽ���a=bʱ���Ⱥų�����
�����ҽ���a=bʱ���Ⱥų�����
�֡�MSN�ʣ�0���У�����0����MSN�� ![]() ��
��
����Ӱ������S���Խ��ʸ�ȫ�����뻭�森
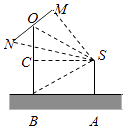
��������1����SC��ֱOB��C�����������֪��CSB= ![]() ����ASB=
����ASB= ![]() ��SA=
��SA= ![]() ����Rt��SAB�пɵ�BA=3����Rt��SCO�У�����֪�ɵ�OC=
����Rt��SAB�пɵ�BA=3����Rt��SCO�У�����֪�ɵ�OC= ![]() ��BC=SA= 3 ����OB=2
��BC=SA= 3 ����OB=2 ![]() ��
��
2��������������SM��SN����SN=a��SM=b���ɣ�1��֪SO=2 ![]() ���������ǵ�����ֵ��ȿɵ�a2+b2=26���������Ҷ����ɵ�cos��MSN=
���������ǵ�����ֵ��ȿɵ�a2+b2=26���������Ҷ����ɵ�cos��MSN=![]() �ٸ��ݻ�������ʽ���cos��MSN>
�ٸ��ݻ�������ʽ���cos��MSN>![]() �����õ�0����MSN��
�����õ�0����MSN�� ![]() .
.