题目内容
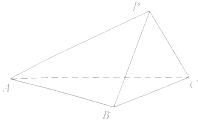
【题目】如图,在四棱锥P﹣ABCD中,PA=PB,PA⊥PB,AB⊥BC,且平面PAB⊥平面ABCD,若AB=2,BC=1, ![]() .
.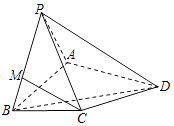
(1)求证:PA⊥平面PBC;
(2)若点M在棱PB上,且PM:MB=3,求证CM∥平面PAD.
【答案】
(1)证明:∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,BC⊥AB,
∴BC⊥平面PAB,又PA平面PAB,
∴BC⊥PA,
又PA⊥PB,PB∩BC=B,PB平面PBC,BC平面PBC,
∴PA⊥平面PBC.
(2)在AB上取点N,使得AN:BN=3,取AB的中点O,连结MN,CN,PO,OD,
∵ ![]() ,
,

∴MN∥PA.
由(1)知BC⊥平面PAB,∴BC⊥BN,
∵BN= ![]() AB=
AB= ![]() ,BC=1,∴tan∠BNC=
,BC=1,∴tan∠BNC= ![]() .
.
∵AD=BD= ![]() ,AB=2,O是AB的中点,
,AB=2,O是AB的中点,
∴OD⊥AB,OA=1,OD= ![]() =2,
=2,
∴tan∠OAD= ![]() ,
,
∴∠BNC=∠OAD,∴CN∥AD,
又MN∩CN,PA∩AD=A,
∴平面MNC∥平面PAD.
又∵CM平面MNC,
∴CM∥平面PAD.
【解析】(1)先利用面面垂直的性质定理可证BC⊥平面PAB,进而可证BC⊥PA,再利用线面垂直的判定定理可证PA⊥平面PBC;(2)先在AB上取点N,使得AN:BN=3,取AB的中点O,连结MN,CN,PO,OD,进而可证MN∥PA,再证CN∥AD,进而可证平面MNC∥平面PAD,从而可证CM∥平面PAD.
【考点精析】关于本题考查的直线与平面平行的判定和平面与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

练习册系列答案
相关题目