题目内容
给出以下五个命题:①若lga+lgb=0(a大于0,b不等于1),则函数f(x)=ax与g(x)=bx的图象关于x轴对称.
②已知函数
 的反函数是y=g(x),则g(x)在(0,+∞)上单调递增.
的反函数是y=g(x),则g(x)在(0,+∞)上单调递增.③为调查参加运动会的1000名运动员的年龄分布情况,从中抽查了100名运动员的档案进行调查,个体是被抽取的每个运动员;
④用独立性检验(2×2列联表)来考察两个变量是否具有相关关系时,计算出的随机变量K2的观测值越大,则说明“X与Y有关系的可能性越大”.
其中正确命题的序号是 .
【答案】分析:对于①由已知的关系等式可以先求出a,b的关系等式,在有指数函数的图形的关系变换即可判断正误.
对于②有已知函数求其反函数的关,然后由函数解析式判断其单调性
对于③有统计知识中的抽样方法可以加以判断正误.
对于④由独立性检验知识可以判断正误.
解答:解:①∵lga+lgb=0,
∴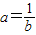 ,
,
∴f(x)=ax=b-x 与g(x)=bx 的图象关于y轴对称,故①错
②∵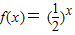
∴f(x)的反函数y=g(x)=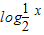 ,此函数应为单调递增函数,故②错
,此函数应为单调递增函数,故②错
③由统计知识知抽样中的个体应为运动员的档案,故③错,
④对变量X与Y的随机变量的K2观测值来说,K2越大,“X与Y有关系”可信程度越大;
故答案为:④
点评:此题考查了指数函数的图象变化,还考查了反函数的概念及对数函数的性质,又考查了统计中的抽样知识,此题主要考查了学生的基本知识与基本技能
对于②有已知函数求其反函数的关,然后由函数解析式判断其单调性
对于③有统计知识中的抽样方法可以加以判断正误.
对于④由独立性检验知识可以判断正误.
解答:解:①∵lga+lgb=0,
∴
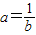 ,
,∴f(x)=ax=b-x 与g(x)=bx 的图象关于y轴对称,故①错
②∵
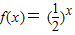
∴f(x)的反函数y=g(x)=
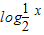 ,此函数应为单调递增函数,故②错
,此函数应为单调递增函数,故②错③由统计知识知抽样中的个体应为运动员的档案,故③错,
④对变量X与Y的随机变量的K2观测值来说,K2越大,“X与Y有关系”可信程度越大;
故答案为:④
点评:此题考查了指数函数的图象变化,还考查了反函数的概念及对数函数的性质,又考查了统计中的抽样知识,此题主要考查了学生的基本知识与基本技能

练习册系列答案
相关题目