题目内容
给出以下五个命题:其中正确命题的序号是
①命题“对任意x∈Rx2+x+1>0”的否定是“存在x∈Rx2+x+1≤0”
②函数f(x)=(
)x-x
在区间(0、1)上存在零点
③“a=1”是“函数y=cos2ax的最小正周期为π”的充分不必要条件
④直线x-2y+5=0与圆x2+y2=8交于A、B两点,则|AB|=2
⑤若直线2ax-bx+8=0(a>0,b>0)平分圆x2+y2+4x-8y+1=0周长则
+
最小值为9.
①②③⑤
①②③⑤
.①命题“对任意x∈Rx2+x+1>0”的否定是“存在x∈Rx2+x+1≤0”
②函数f(x)=(
| 1 |
| 2 |
| 1 |
| 3 |
③“a=1”是“函数y=cos2ax的最小正周期为π”的充分不必要条件
④直线x-2y+5=0与圆x2+y2=8交于A、B两点,则|AB|=2
| 2 |
⑤若直线2ax-bx+8=0(a>0,b>0)平分圆x2+y2+4x-8y+1=0周长则
| 8 |
| a |
| 2 |
| b |
分析:根据全称、特称命题的否定方法,可判断①的真假;根据零点存在定理可得②的真假;对于③,利用最小正周期为π,求出a,即可判断选项;对于④,先求出圆心到直线的距离d,再利用弦长公式求得弦长|AB|;⑤由题意可知圆x2+y2+4x-8y+1=0的圆心(-2,4)在直线2ax-bx+8=0上,可得a+b=2,而
+
=
(
+
)(a+b),展开利用基本不等式可求最小值.
| 8 |
| a |
| 2 |
| b |
| 1 |
| 2 |
| 8 |
| a |
| 2 |
| b |
解答:解:①对,因为命题“?x∈R,x2+x+1>0”的否定是:“?x∈R,x2+x+1≤0”.
②中f(0)=1>0,f(1)=
-1<0,根据零点存在定理,
得函数f(x)=(
)x-x
在区间(0、1)上存在零点.可知②正确;
③:函数y=cos2ax,它的周期是
=π,a=±1,
显然“a=1”可得“函数y=cos2ax的最小正周期为π”,后者推不出前者,
∴“a=1”是“函数y=cos2ax的最小正周期为π”的充分不必要条件,正确;
④:圆x2+y2=8的圆心为(0,0),半径等于2
,圆心不在直线x-2y+5=0上,
由圆的性质可知,|AB|<2
,故④不对;
⑤:由圆的性质可知,直线2ax-bx+8=0即是圆的直径所在的直线方程,
∵圆x2+y2+4x-8y+1=0的圆心(-2,4)在直线2ax-bx+8=0上
∴-4a-4b+8=0即a+b=2,
∵
+
=
(
+
)(a+b)=
(10+
+
)≥
(10+8)=9,
当且仅当
=
取等号,
∴
+
的最小值9,正确.
故答案为:①②③⑤.
②中f(0)=1>0,f(1)=
| 1 |
| 2 |
得函数f(x)=(
| 1 |
| 2 |
| 1 |
| 3 |
③:函数y=cos2ax,它的周期是
| 2π |
| |2a| |
显然“a=1”可得“函数y=cos2ax的最小正周期为π”,后者推不出前者,
∴“a=1”是“函数y=cos2ax的最小正周期为π”的充分不必要条件,正确;
④:圆x2+y2=8的圆心为(0,0),半径等于2
| 2 |
由圆的性质可知,|AB|<2
| 2 |
⑤:由圆的性质可知,直线2ax-bx+8=0即是圆的直径所在的直线方程,
∵圆x2+y2+4x-8y+1=0的圆心(-2,4)在直线2ax-bx+8=0上
∴-4a-4b+8=0即a+b=2,
∵
| 8 |
| a |
| 2 |
| b |
| 1 |
| 2 |
| 8 |
| a |
| 2 |
| b |
| 1 |
| 2 |
| 8b |
| a |
| 2a |
| b |
| 1 |
| 2 |
当且仅当
| 8b |
| a |
| 2a |
| b |
∴
| 8 |
| a |
| 2 |
| b |
故答案为:①②③⑤.
点评:本题考查的知识点是命题的真假判断,熟练掌握相关的基本概念是关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
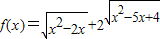 的最小值为l+2
的最小值为l+2 ;
; ,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;
,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题; ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件; 为不共线向量,又
为不共线向量,又 ,若
,若 ,则S2012=2013.
,则S2012=2013.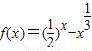 在区间(0、1)上存在零点
在区间(0、1)上存在零点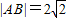
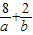 最小值为9.
最小值为9.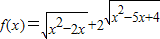 的最小值为l+2
的最小值为l+2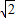 ;
; ,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;
,且|x1|>|x2|时,有f (x1)>f(x2)”是真命题;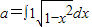 ”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;
”是函数“y=cos2(ax)-sin2(ax)的最小正周期为4”的充要条件;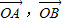 为不共线向量,又
为不共线向量,又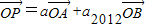 ,若
,若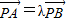 ,则S2012=2013.
,则S2012=2013.