题目内容

四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
AD,∠BAD=60°,E,F分别为AD,PC的中点.
(1)求证:EF∥面PAB
(2)求证:EF⊥面PBD
(3)求二面角D-PA-B的余弦值.
分析:(1)取PB的中点为M连结AM,MF,利用已知条件证明AMFE是平行四边形,即可求证EF∥面PAB
(2)利用已知条件通过直线与平面垂直的判定定理证明EF⊥面PBD
(3)通过(2),利用BD⊥平面PAB,作BN⊥PA于N,说明∠BND就是二面角D-PA-B的平面角,然后求二面角D-PA-B的余弦值.
解答: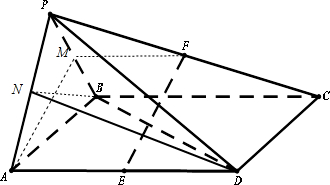
解:(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,所以FM
BC,又ABCD是平行四边形,
E为AD的中点,所以AMFE是平行四边形,
所以EF∥面PAB.
(2)因为
PA=PB=AB=AD,M是PB的中点,所以AM⊥PB,∠BAD=60°,所以AB⊥BD,
因为面PAB⊥面ABCD,所以BD⊥平面PAB,所以AM⊥BD,
又PB∩BD=B,所以AM⊥面PBD.EF∥AM,
所以EF⊥面PBD.
(3)由(2)可知BD⊥平面PAB,作BN⊥PA于N,
显然N是PA的中点,连结ND,
则∠BND就是二面角D-PA-B的平面角,
设
PA=PB=AB=AD=2,所以AN=1,AD=4,BD=
=
,
BN=
=
,所以ND=
=
,
所以二面角D-PA-B的余弦值为:
=
=
.
点评:本题考查空间几何体中直线与平面平行的判定定理以及直线与平面垂直的判定定理的应用,直线与平面设出角的求法,空间向量的数量积的应用,考查逻辑推理能力与计算能力.
练习册系列答案
相关题目
 四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,面PAB⊥面ABCD,PA=PB=AB= 解:(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,所以FM
解:(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,所以FM 解:(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,所以FM
解:(1)证明:取PB的中点为M连结AM,MF,因为F为PC的中点,所以FM
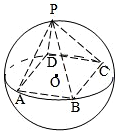 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若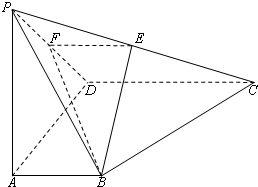 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AB,CD⊥DA,CD=2AB,PA⊥底面ABCD,E、F分别为PC,PD的中点,PA=AD=AB.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AB,CD⊥DA,CD=2AB,PA⊥底面ABCD,E、F分别为PC,PD的中点,PA=AD=AB.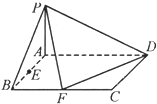 已知四棱锥P-ABCD底面ABCD是矩形,PA丄平面ABCD,AD=4,AB=2,E,F分别是线段AB和BC的中点.
已知四棱锥P-ABCD底面ABCD是矩形,PA丄平面ABCD,AD=4,AB=2,E,F分别是线段AB和BC的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1. (2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知
(2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知