Question

【题目】设函数，其中，角的顶点与坐标原点重合，始边与轴非负半轴重合，终边经过点，且.

（Ⅰ）若点的坐标为，求的值；

（Ⅱ）若点为线性约束条件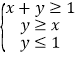所围成的平面区域上的一个动点，试确定角的取值范围，并求函数的最小值和最大值．

Answer 1

【答案】（1）2（2）函数的最小值为1，最大值为

【解析】

（1）若P点的坐标为，根据三角函数的定义，可得，，代入可得的值；
（Ⅱ））若点为线性约束条件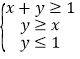上的一个动点，则，结合正弦函数的图象和性质可得函数f（a）的最小值及取得最小值时的α的值．

（1）∵点的坐标为，可得，

∴由三角函数的定义，得，，

故.

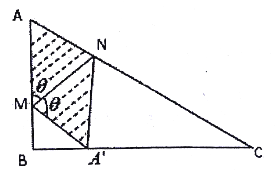
（2）不等式组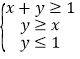表示的平面区域为如图所示的阴影2部分的及其内部区域，

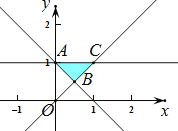
其中、，，

∵为区域内一个动点，且为角终边上的一点，

∴运动点，可得当与点重合时，取得最大值为；

当与线段上一点重合时，取得最小值为．由此可得.

∵，

∴由，可得，

当即时，取得最小值；

当即时，取得最大值.

综上所述，函数的最小值为1，最大值为.