题目内容
在正三棱锥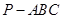 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,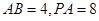 ,过
,过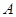 作与
作与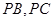 分别交于
分别交于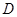 和
和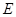 的截面,则截面
的截面,则截面
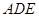 的周长的最小值是 ( )
的周长的最小值是 ( )
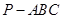 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,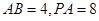 ,过
,过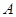 作与
作与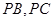 分别交于
分别交于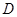 和
和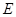 的截面,则截面
的截面,则截面
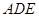 的周长的最小值是 ( )
的周长的最小值是 ( )| A.9 | B.10 | C.11 | D.12 |
C
分析:利用正三棱锥P-ABC的侧面展开图,即可将求△ADE的周长的最小值问题转化为求展开图中线段的长的问题,进而在三角形中利用解三角形的知识计算即可
解答:解:此正三棱锥的侧面展开图如图:则△ADE的周长为AD+DE+EA′,由于两点之间线段最短,
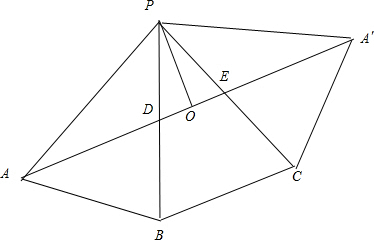
∴当D、E处于如图位置时,截面△ADE的周长最小,即为AA′的长
设∠APB=α,过P作PO⊥AA′,则O为AA′中点,∠APO=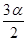 ,
,
在等腰三角形PAB中,sin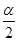 =
=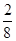 =
=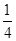 ,cos
,cos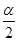 =
=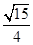
∴cosα=1-2sin2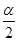 =
=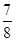 ,sinα=2sin
,sinα=2sin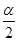 ?cos
?cos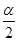 =
=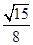
∴sin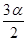 =sin(α+
=sin(α+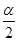 )=sinαcos
)=sinαcos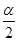 +cosαsin
+cosαsin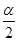 =
=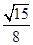 ×
×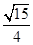 +
+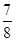 ×
×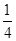 =
=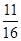
∴AA′=2AO=2AP×sin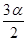 =16×
=16×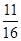 =11
=11
故选C
解答:解:此正三棱锥的侧面展开图如图:则△ADE的周长为AD+DE+EA′,由于两点之间线段最短,

∴当D、E处于如图位置时,截面△ADE的周长最小,即为AA′的长
设∠APB=α,过P作PO⊥AA′,则O为AA′中点,∠APO=
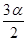 ,
,在等腰三角形PAB中,sin
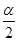 =
=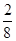 =
=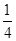 ,cos
,cos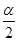 =
=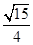
∴cosα=1-2sin2
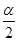 =
=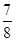 ,sinα=2sin
,sinα=2sin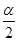 ?cos
?cos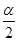 =
=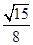
∴sin
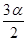 =sin(α+
=sin(α+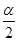 )=sinαcos
)=sinαcos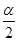 +cosαsin
+cosαsin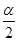 =
=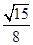 ×
×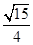 +
+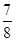 ×
×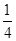 =
=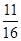
∴AA′=2AO=2AP×sin
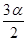 =16×
=16×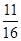 =11
=11故选C

练习册系列答案
相关题目
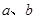 是异面直线,直线
是异面直线,直线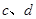 分别与
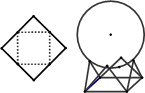
分别与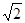 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1鸡蛋(视为球体)放入 其 中,则鸡蛋中心(球心)与蛋巢底面的距离为 ( )
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1鸡蛋(视为球体)放入 其 中,则鸡蛋中心(球心)与蛋巢底面的距离为 ( )



 知
知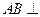 平面
平面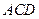 ,
,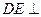 平面
平面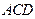 ,△
,△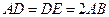 ,
,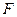 为
为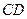 的中点.
的中点.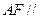 平面
平面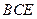
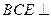 平面
平面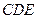 ;
;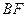 和平面
和平面
 ,则
,则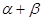 满足( )
满足( )



 知四棱锥
知四棱锥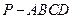 的底面为直角梯形,AD∥BC,∠BCD=90°
的底面为直角梯形,AD∥BC,∠BCD=90° ,PA=PB,PC=PD
,PA=PB,PC=PD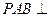 平面ABCD;
平面ABCD;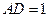
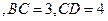 ,且侧面
,且侧面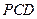 的面积为8,求四棱锥
的面积为8,求四棱锥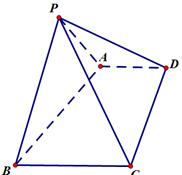
 的角,
的角, ,则OP与平面AOB所成的角等于( )
,则OP与平面AOB所成的角等于( )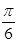 B.
B. D.
D.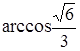
 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ,
, ,则
,则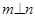 ②若
②若 ,
, ,
,
 ,
, ④若
④若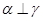 ,
, ,则
,则
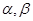 是两个不同的平面,m,n是两条不同的直线,给出下列命题:
是两个不同的平面,m,n是两条不同的直线,给出下列命题: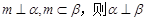 ; ②若
; ②若 ;
;  相交;
相交; 其中正确的命题是 ( )
其中正确的命题是 ( )